TOANMATH.com giới thiệu đến các em học sinh khối 12 tài liệu chuyên đề hình học tọa độ Oxyz (phiên bản đặc biệt), tài liệu gồm 901 trang trình bày đầy đủ lý thuyết, dạng toán và bài tập trắc nghiệm chủ đề phương pháp tọa độ trong không gian (Hình học 12 chương 3), tài liệu được biên soạn bởi thầy Đặng Việt Đông.
CHỦ ĐỀ 1. HỆ TRỤC TỌA ĐỘ
Dạng 1: Tìm tọa độ điểm, tọa độ vec tơ thỏa điều kiện cho trước.
Dạng 2: Tính độ dài đoạn thẳng.
Dạng 3: Xét sự cùng phương, sự đồng phẳng.
Dạng 4: Bài toán về tích vô hướng, góc và ứng dụng.
Dạng 5: Bài toán về tích có hướng và ứng dụng.
CHỦ ĐỀ 2. PHƯƠNG TRÌNH MẶT CẦU
Dạng 1: Tìm tâm và bán kính, điều kiện xác định mặt cầu.
Dạng 2: Phương trình mặt cầu biết tâm, dễ tính bán kính (chưa học phương trình mặt phẳng).
Dạng 3: Phương trình mặt cầu biết 2 đầu mút của đường kính.
Dạng 4: Phương trình mặt cầu ngoại tiếp tứ diện.
Dạng 5: Phương trình mặt cầu qua nhiều điểm, thỏa điều kiện.
Dạng 6: Phương trình mặt cầu biết tâm, tiếp xúc với mặt phẳng.
Dạng 7: Phương trình mặt cầu biết tâm và đường tròn trên nó.
Dạng 8: Phương trình mặt cầu biết tâm và điều kiện của dây cung.
Dạng 9: Phương trình mặt cầu biết tâm thuộc d, thỏa điều kiện.
Dạng 10: Phương trình mặt cầu biết tâm thuộc mặt phẳng, thỏa điều kiện.
Dạng 11: Phương trình mặt cầu biết tâm, thỏa điều kiện khác.
Dạng 12: Phương trình mặt cầu thỏa mãn điều kiện đối xứng.
Dạng 13: Toán max – min liên quan đến mặt cầu.
Dạng 14: Điểm thuộc mặt cầu thỏa điều kiện.
[ads]
CHỦ ĐỀ 3. PHƯƠNG TRÌNH MẶT PHẲNG (CHƯA HỌC PHƯƠNG TRÌNH ĐƯỜNG THẲNG)
Dạng 1: Tìm vectơ pháp tuyến, các vấn đề về lý thuyết.
Dạng 2: Phương trình mặt phẳng trung trực của đoạn thẳng.
Dạng 3: Phương trình mặt phẳng qua 1 điểm, dễ tìm vectơ pháp tuyến (không dùng tích có hướng).
Dạng 4: Phương trình mặt phẳng qua 1 điểm, vectơ pháp tuyến tìm bằng tích có hướng.
Dạng 5: Phương trình mặt phẳng qua 1 điểm, tiếp xúc với mặt cầu.
Dạng 6: Phương trình mặt phẳng qua 1 điểm, cắt mặt cầu.
Dạng 7: Phương trình mặt phẳng qua 1 điểm, thỏa điều kiện về góc, khoảng cách.
Dạng 8: Phương trình mặt phẳng qua 1 điểm, thỏa điều kiện khác.
Dạng 9: Phương trình mặt phẳng qua 2 điểm, vectơ pháp tuyến tìm bằng tích có hướng.
Dạng 10: Phương trình mặt phẳng qua 2 điểm, thỏa điều kiện về góc, khoảng cách.
Dạng 11: Phương trình mặt phẳng qua 2 điểm, thỏa điều kiện khác.
Dạng 12: Phương trình mặt phẳng qua 3 điểm không thẳng hàng.
Dạng 13: Phương trình mặt phẳng theo đoạn chắn.
Dạng 14: Phương trình mặt phẳng song song với mặt phẳng, thỏa điều kiện.
CHỦ ĐỀ 4. PHƯƠNG TRÌNH MẶT PHẲNG (CÓ SỬ DỤNG PHƯƠNG TRÌNH ĐƯỜNG THẲNG)
Dạng 1: Tìm vectơ pháp tuyến, các vấn đề về lý thuyết.
Dạng 2: Phương trình mặt phẳng qua 1 điểm, dễ tìm vectơ pháp tuyến (không dùng tích có hướng).
Dạng 3: Phương trình mặt phẳng qua 1 điểm, vectơ pháp tuyến tìm bằng tích có hướng (đường – mặt).
Dạng 4: Phương trình mặt phẳng qua 1 điểm và chứa đường thẳng.
Dạng 5: Phương trình mặt phẳng qua 1 điểm, thỏa điều kiện khác.
Dạng 6: Phương trình mặt phẳng qua 2 điểm, vectơ pháp tuyến tìm bằng tích có hướng.
Dạng 7: Phương trình mặt phẳng qua 2 điểm, thỏa điều kiện về góc, khoảng cách.
Dạng 8: Phương trình mặt phẳng chứa 1 đường thẳng, thỏa điều kiện với đường thẳng khác.
Dạng 9: Phương trình mặt phẳng chứa 1 đường thẳng, thỏa điều kiện với mặt phẳng.
Dạng 10: Phương trình mặt phẳng chứa 1 đường thẳng, thỏa điều kiện về góc, khoảng cách.
Dạng 11: Phương trình mặt phẳng chứa 1 đường thẳng, thỏa điều kiện với mặt cầu.
Dạng 12: Phương trình mặt phẳng theo đoạn chắn thỏa điều kiện với đường thẳng.
Dạng 13: Phương trình mặt phẳng song song với mặt phẳng, thỏa điều kiện.
Dạng 14: Toán max – min liên quan đến mặp phẳng.
Dạng 15: Điểm thuộc mặt phẳng thỏa điều kiện.
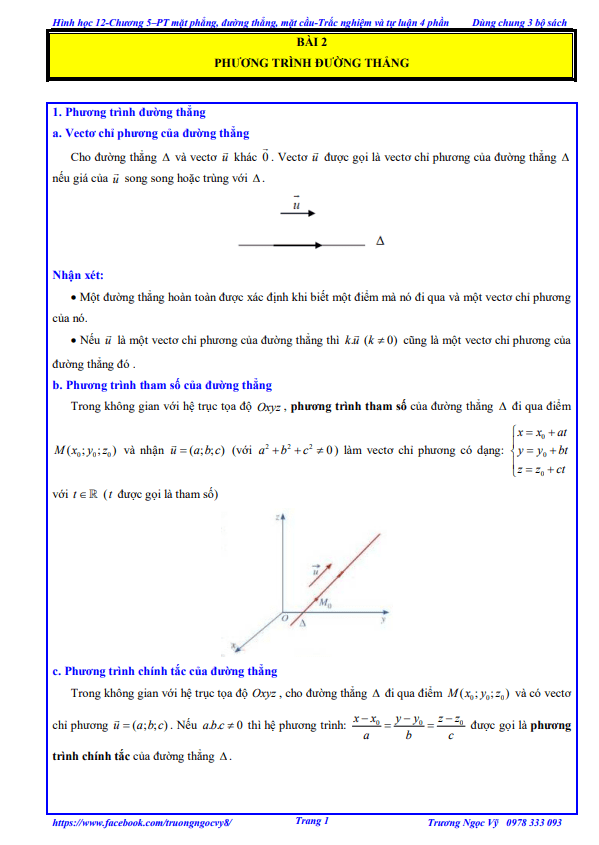
CHỦ ĐỀ 5. PHƯƠNG TRÌNH ĐƯỜNG THẲNG
Dạng 1: Tìm vectơ chỉ phương, các vấn đề về lý thuyết.
Dạng 2: Phương trình đường thẳng qua 1 điểm, dễ tìm vectơ chỉ phương (không dùng tích có hướng).
Dạng 3: Phương trình đường thẳng qua 1 điểm, vectơ chỉ phương tìm bằng tích có hướng (cho 2 mặt phẳng).
Dạng 4: Phương trình đường thẳng qua 1 điểm, vectơ chỉ phương tìm bằng tích có hướng (cho 2 đường thẳng).
Dạng 5: Phương trình đường thẳng qua 1 điểm, vectơ chỉ phương tìm bằng tích có hướng (cho đường thẳng + mặt phẳng).
Dạng 6: Phương trình đường thẳng qua 1 điểm, cắt d1, có liên hệ với d2.
Dạng 7: Phương trình đường thẳng qua 1 điểm, cắt d, có liên hệ với mặt phẳng (P).
Dạng 8: Phương trình đường thẳng qua 1 điểm, cắt d1 lẫn d2.
Dạng 9: Phương trình đường thẳng qua 1 điểm, vừa cắt – vừa vuông góc với d.
Dạng 10: Phương trình đường thẳng qua 1 điểm, vuông góc với d, thỏa điều kiện khoảng cách.
Dạng 11: Phương trình đường thẳng qua 1 điểm, thỏa điều kiện khác.
Dạng 12: Phương trình đường thẳng cắt 2 đường thẳng d1, d2, thỏa điều kiện khác.
Dạng 13: Phương trình đường thẳng nằm trong (P), vừa cắt vừa vuông góc với d.
Dạng 14: Phương trình đường thẳng thỏa điều kiện đối xứng.
Dạng 15: Phương trình giao tuyến của 2 mặt phẳng.
Dạng 16: Phương trình đường vuông góc chung của hai đường thẳng chéo nhau.
Dạng 17: Phương trình hình chiếu vuông góc của d lên (P).
Dạng 18: Toán max – min liên quan đến đường thẳng.
Dạng 19: Điểm thuộc đường thẳng thỏa điều kiện.
CHỦ ĐỀ 6. TOÁN TỔNG HỢP VỀ ĐƯỜNG THẲNG – MẶT PHẲNG – MẶT CẦU
Dạng 1: Xét vị trí tương đối giữa 2 mặt phẳng.
Dạng 2: Xét vị trí tương đối giữa 2 đường thẳng.
Dạng 3: Xét vị trí tương đối giữa đường thẳng và mặt phẳng.
Dạng 4: Xét vị trí tương đối giữa mặt phẳng và mặt cầu.
Dạng 5: Xét vị trí tương đối giữa đường thẳng và mặt cầu.
Dạng 6: Góc giữa hai mặt phẳng.
Dạng 7: Góc giữa hai đường thẳng.
Dạng 8: Góc giữa đường thẳng và mặt phẳng.
Dạng 9: Khoảng cách từ 1 điểm đến 1 mặt phẳng.
Dạng 10: Khoảng cách từ 1 điểm đến 1 đường thẳng.
Dạng 11: Khoảng cách giữa hai đối tượng song song.
Dạng 12: Khoảng cách giữa hai đường thẳng chéo nhau.
Dạng 13: Tìm giao điểm của đường thẳng và mặt phẳng.
Dạng 14: Tìm giao điểm của hai đường thẳng cắt nhau.
Dạng 15: Tìm giao điểm của đường thẳng và mặt cầu.
Dạng 16: Hình chiếu vuông góc của điểm lên đường, mặt (và ứng dụng).
Dạng 17: Tìm điểm thỏa điều kiện đối xứng.
CHỦ ĐỀ 7. MIN – MAX VÀ TOÁN THỰC TẾ
Dạng 1: Toán max – min tổng hợp.
Dạng 2: Toán thực tế.