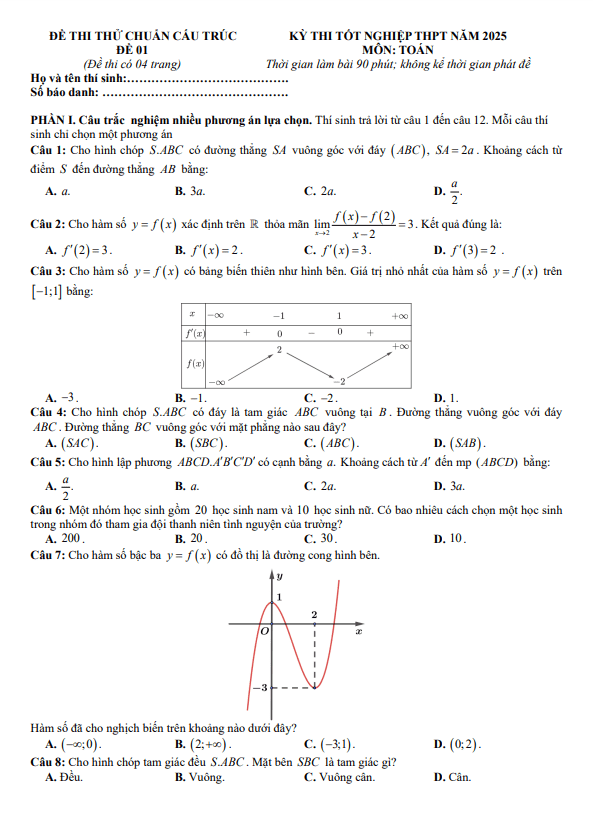
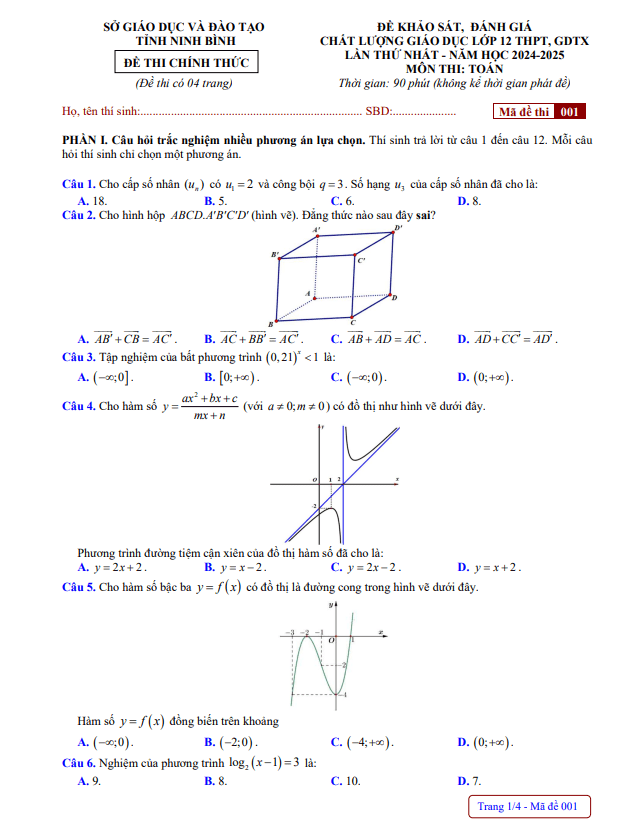
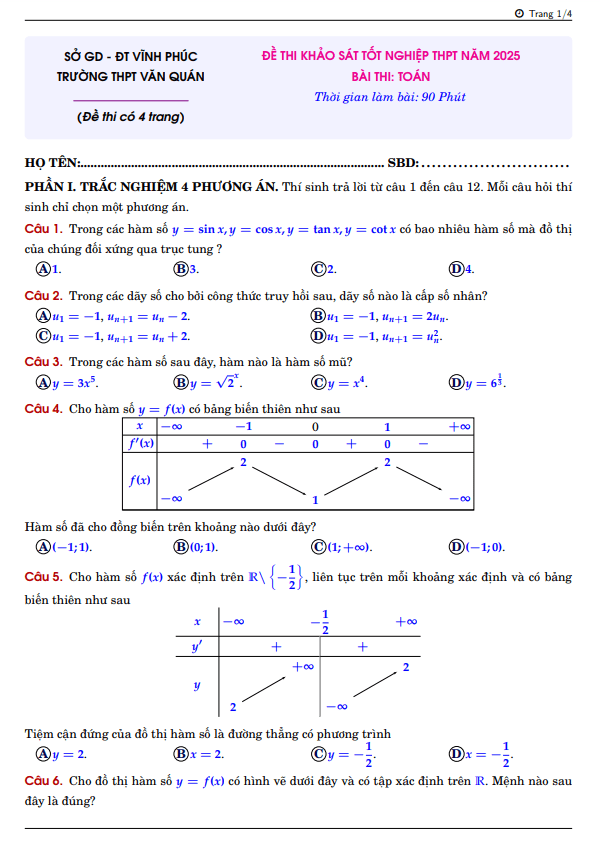
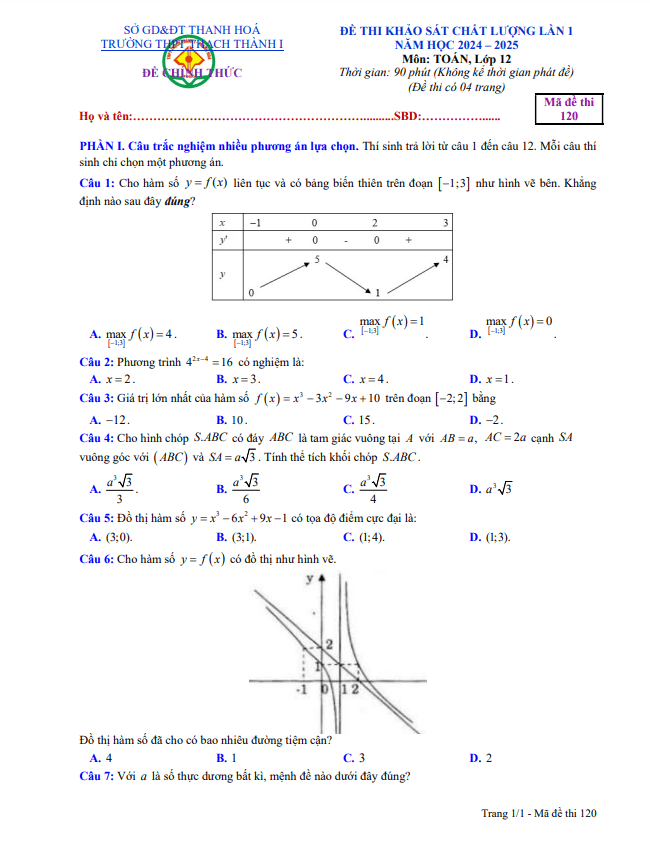
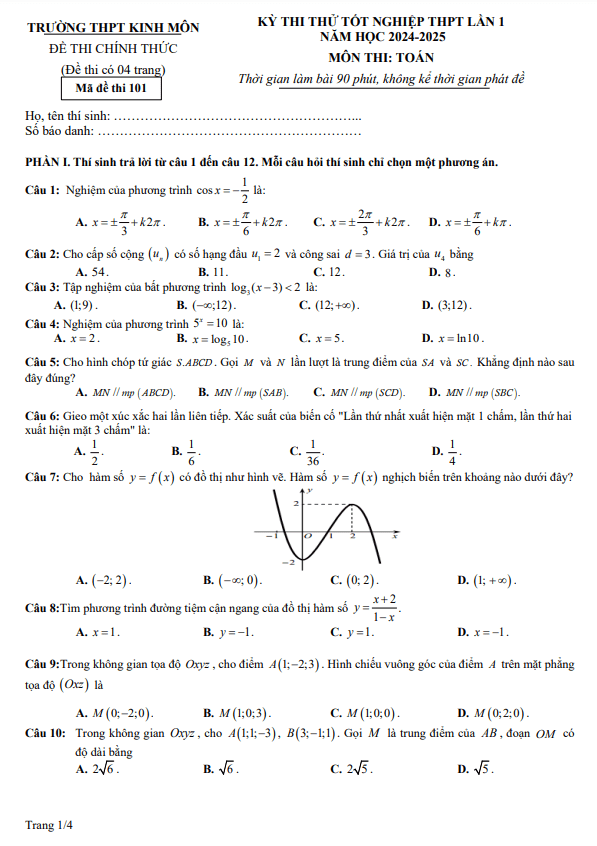TOANMATH.com giới thiệu đến các em nội dung đề KSCL môn Toán thi ĐH 2019 trường THPT Hàm Rồng – Thanh Hóa, kỳ thi được tổ chức vào Chủ Nhật, ngày 13 tháng 01 năm 2019 nhằm kiểm tra chất lượng ôn tập chuẩn bị cho kỳ thi Trung học Phổ thông Quốc gia môn Toán năm học 2018 – 2019 của các em học sinh khối 12, đề có mã đề 061 gồm 06 trang với 50 câu trắc nghiệm, thời gian làm bài 90 phút.
Trích dẫn đề KSCL môn Toán thi ĐH 2019 trường THPT Hàm Rồng – Thanh Hóa:
+ Trong không gian với hệ trục toạ độ Oxyz, cho 3 điểm A(1;0;1); B(3;-2;0); C(1;2;-2). Gọi (P) là mặt phẳng đi qua A sao cho tổng khoảng cách từ B và C đến (P) lớn nhất biết rằng (P) không cắt đoạn BC. Khi đó véc tơ pháp tuyến của mặt phẳng (P) là?
+ Đầu mỗi tháng anh A gửi vào ngân hàng 3 triệu đồng với lãi suất kép là 0,6% mỗi tháng. Hỏi sau ít nhất bao nhiêu tháng (khi ngân hàng đã tính lãi) thì anh A có được số tiền cả lãi và gốc nhiều hơn 100
triệu biết lãi suất không đổi trong quá trình gửi.
A. 30 tháng. B. 40 tháng. C. 35 tháng. D. 31 tháng.
[ads]
+ Cho tứ diện ABCD, trên các cạnh BC, BD, AC lần lượt lấy các điểm M, N, P sao cho BC = 3BM, BD = 3/2.BN, AC = 2AP. Mặt phẳng (MNP) chia khối tứ diện ABCD thành hai phần có thể tích là V1, V2. Tính tỉ số V1/V2.