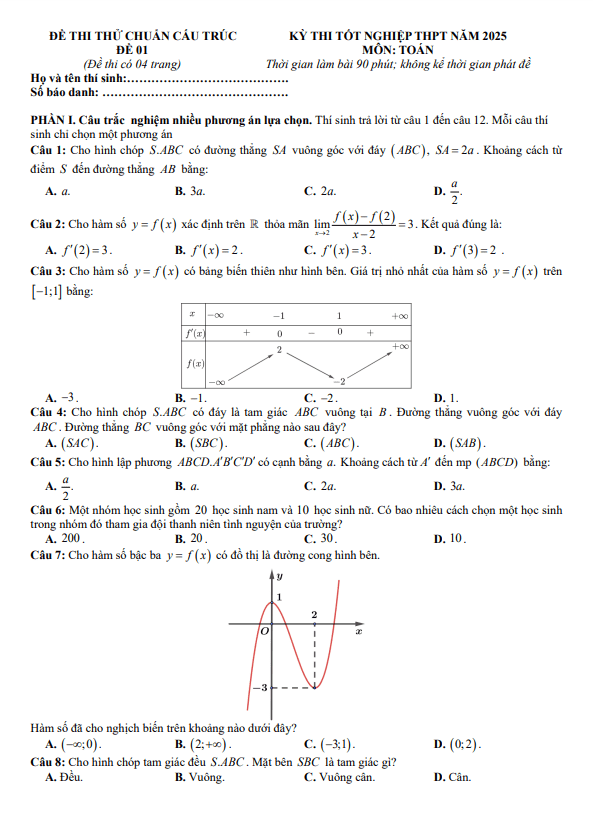
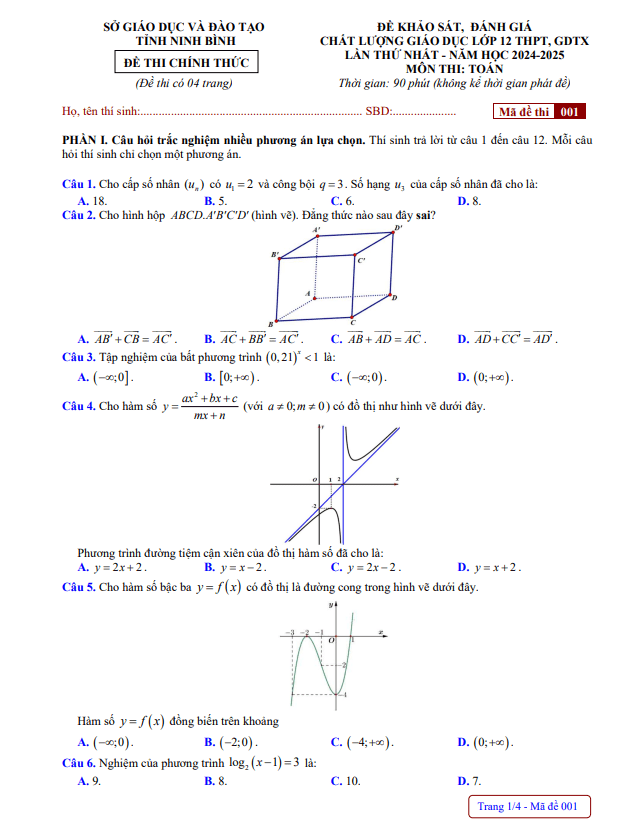
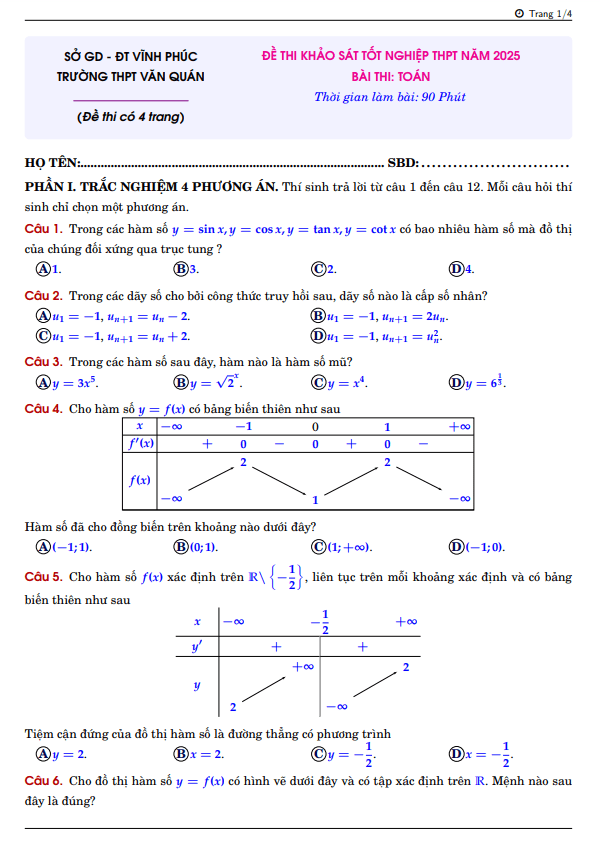
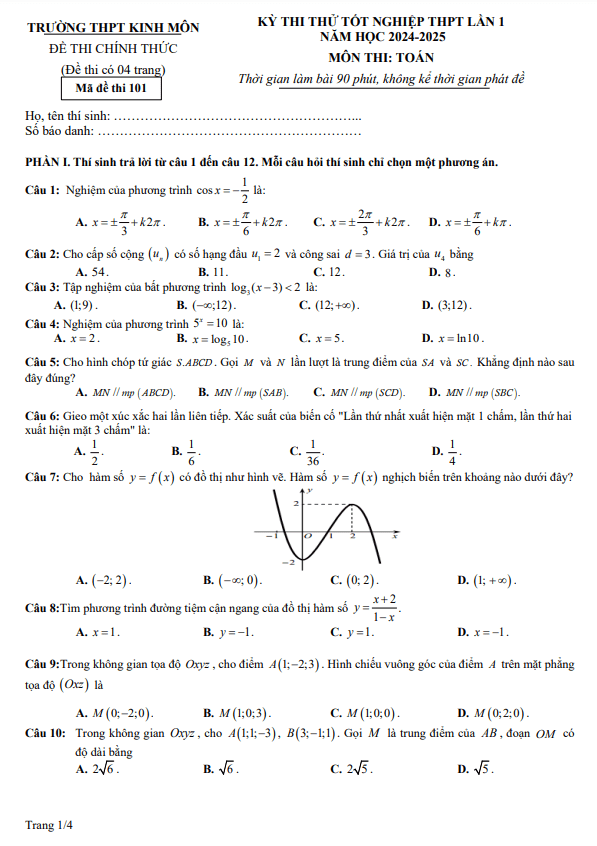Chủ Nhật ngày 05 tháng 07 năm 2020, trường THPT chuyên Quốc học Huế, tỉnh Thừa Thiên Huế tổ chức kỳ thi thử tốt nghiệp Trung học Phổ thông môn Toán lần thứ hai năm học 2019 – 2020 dành cho học sinh khối 12.
Đề thi thử tốt nghiệp THPT 2020 môn Toán lần 2 trường chuyên Quốc học Huế mã đề 143 gồm có 06 trang với 50 câu hỏi và bài toán dạng trắc nghiệm, thời gian làm bài 90 phút, đề thi có đáp án mã đề 143, 295, 387, 415.
Trích dẫn đề thi thử tốt nghiệp THPT 2020 môn Toán lần 2 trường chuyên Quốc học Huế:
+ Biết rằng các số log a; log b; log c theo thứ tự đó lập thành cấp số cộng, đồng thời log a – log 2b; log 2b – log 3c; log 3c – log a theo thứ tự đó cũng tạo thành một cấp số cộng. Tìm khẳng định đúng?
A. Không có tam giác nào có ba cạnh là a, b, c.
B. a, b, c là ba cạnh của một tam giác tù.
C. a, b, c là ba cạnh của một tam giác vuông.
D. a, b, c là ba cạnh của một tam giác nhọn.
[ads]
+ Giả sử hàm số y = mx^4 – (m^2 + 2)x^2 + (m^3 + 11m)/9 có đồ thị (C) và hàm số y = x^2 có đồ thị (C) cắt nhau tại bốn điểm phân biệt. Biết rằng hình phẳng (H) giới hạn (C) và (C) là hợp của ba hình phẳng (H1), (H2), (H3) có diện tích tương ứng là S1, S2, S3 trong đó 0 ≤ S1 ≤ S2 ≤ S3 và các hình phẳng (H1), (H2), (H3) đôi một giao nhau tại không quá một điểm. Gọi T là tập hợp các giá trị của m sao cho S3 = S1 + S2. Tính tổng bình phương các phần tử của T.
+ Cắt một vật thể (T) bởi hai mặt phẳng (P) và (Q) vuông góc với trục Ox lần lượt tại các điểm có hoành độ x = a và x = b (a < b) (xem hình). Một mặt phẳng tùy ý vuông góc với Ox tại điểm có hoành độ x (a ≤ x ≤ b) cắt (T) theo thiết diện có diện tích là S(x). Giả sử S(x) liên tục trên đoạn [a;b]. Khi đó thể tích V của phần vật thể (T) giới hạn bởi hai mặt phẳng (P) và (Q) được tính bởi công thức nào sau đây?