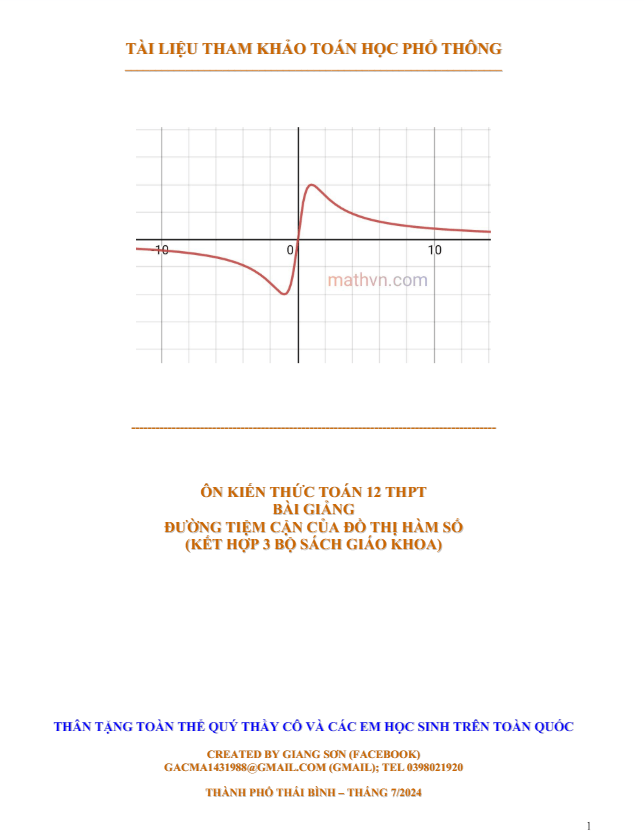
Tài liệu gồm 34 trang, tóm tắt lý thuyết cơ bản cần nắm và hướng dẫn phương pháp giải các dạng bài tập trắc nghiệm vận dụng cao (VDC / nâng cao / khó) đường tiệm cận của đồ thị hàm số, phù hợp với đối tượng học sinh khá – giỏi khi học chương trình Giải tích 12 chương 1 (ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số) và ôn thi điểm 8 – 9 – 10 trong kỳ thi tốt nghiệp THPT môn Toán.
Các dạng bài tập trắc nghiệm VDC đường tiệm cận của đồ thị hàm số:
A. KIẾN THỨC CƠ BẢN CẦN NẮM
B. PHÂN DẠNG VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1. Xác định các đường tiệm cận dựa vào định nghĩa.
Dạng 2. Tiệm cận của đồ thị hàm số y = (ax + b)/(cx + d).
Dạng 3. Tiệm cận của đồ thị hàm số phân thức hữu tỷ.
Dạng 4. Tiệm cận của đồ thị hàm số vô tỷ.
Dạng 5. Biết đồ thị, bảng biến thiên của hàm số y = f(x), xác định tiệm cận của đồ thị hàm số y = A/g(x) với A là số thực khác 0, g(x) xác định theo f(x).
Dạng 6. Biết đồ thị, bảng biến thiên của hàm số y = f(x), xác định tiệm cận của đồ thị hàm số y = φ(x)/g(x) với φ(x) là một biểu thức theo x, g(x) là biểu thức theo f(x).
Dạng 7. Biện luôn số đường tiệm cận của đồ thị hàm số phân thức y = f(x)/g(x) với f(x) và g(x) là các đa thức.
Dạng 8. Biện luận số đường tiệm cận của đồ thị hàm số chứa căn thức.
Dạng 9. Biện luận số đường tiệm cận của đồ thị hàm ẩn.
Dạng 10. Bài toán liên quan đến đường tiệm cận của đồ thị hàm số y = (ax + b)/(cx + d).
Dạng 11. Bài toán về khoảng cách từ điểm trên đồ thị hàm số y = (ax + b)/(cx + d) đến các đường tiệm cận.
Dạng 12. Bài toán liên quan giữa tiếp tuyến và tiệm cận của đồ thị hàm số y = (ax + b)/(cx + d).
Xem thêm:
+ Các dạng toán về hàm ẩn liên quan đến tiệm cận của hàm số