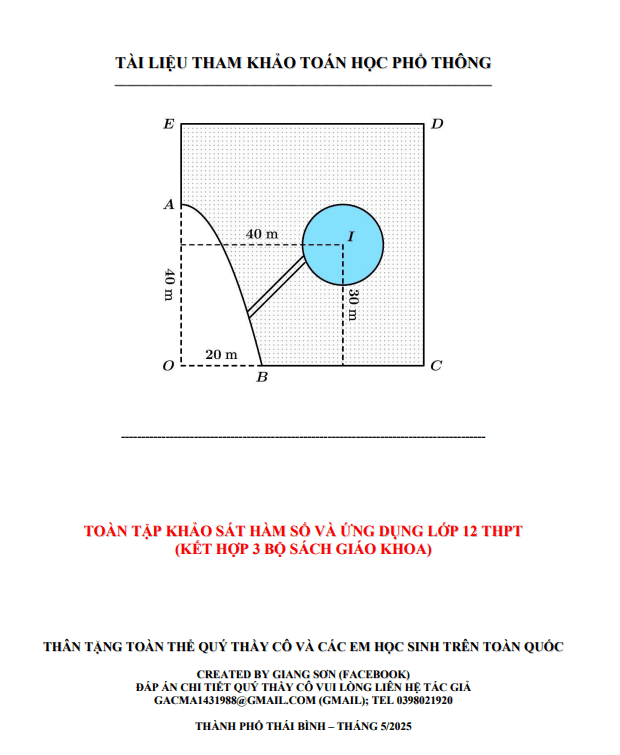
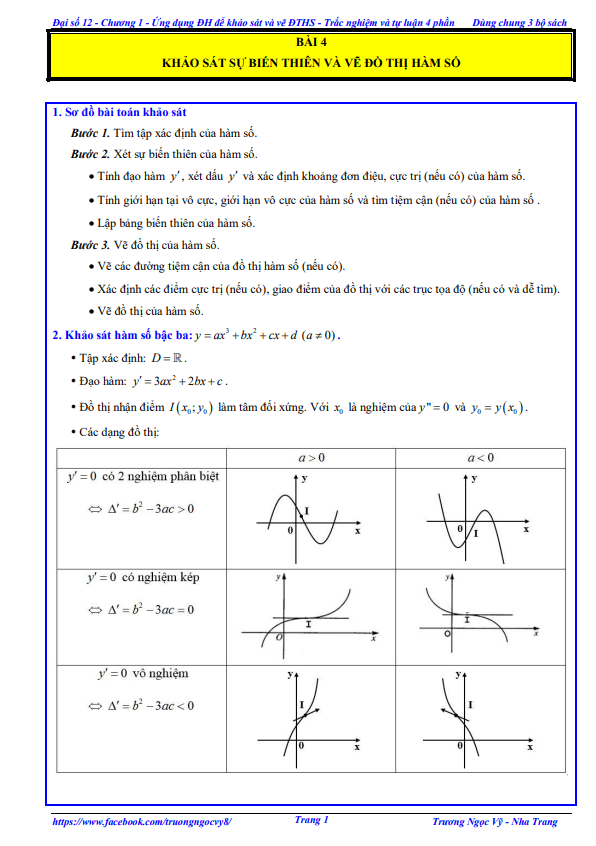
Chuyên đề nâng cao về hàm số do thầy Lê Quang Xe biên soạn gồm 184 trang, giúp học sinh lớp 12 tham khảo khi học chương trình Toán 12 phần Giải tích chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số.

MỤC LỤC:
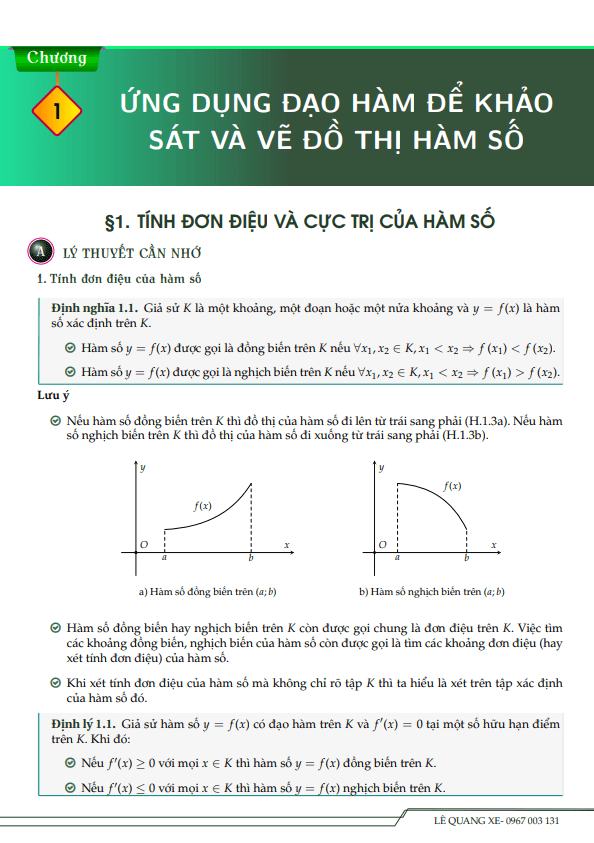
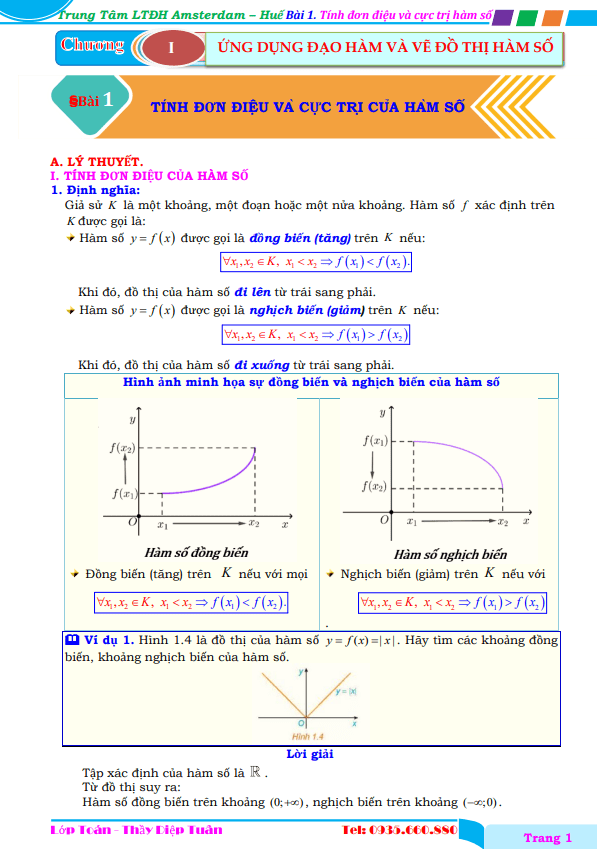
§1 – TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ 1.
A Lý thuyết 1.
B Ví dụ 2.
C Một số dạng toán cơ bản 7.
+ Dạng 1. Cơ bản về tính đơn điệu của hàm số 7.
+ Dạng 2. Tính đơn điệu của hàm hợp 12.
+ Dạng 3. Tính đơn điệu của hàm giá trị tuyệt đối 29.
§2 – CỰC TRỊ CỦA HÀM SỐ 39.
A Lý thuyết 39.
B Ví dụ 40.
C Một số dạng toán cơ bản 45.
+ Dạng 1. Cơ bản về cực trị của hàm số 45.
+ Dạng 2. Cực trị của hàm tổng và hàm hợp 48.
+ Dạng 3. Bài toán truy tìm hàm ngược 60.
+ Dạng 4. Cực trị hàm số chứa dấu giá trị tuyệt đối 65.
+ Dạng 5. Cực trị tại một điểm cho trước 76.
§3 – GIÁ TRỊ LỚN NHẤT – GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ 87.
A Lý thuyết 87.
B Ví dụ minh họa 88.
C Một số dạng toán cơ bản 93.
+ Dạng 1. Cơ bản về Max – Min của hàm số 93.
+ Dạng 2. Min – Max của hàm đa thức và BPT 96.
+ Dạng 3. Min – Max của hàm hợp 99.
+ Dạng 4. Giá trị lớn nhất, giá trị nhỏ nhất của hàm số chứa dấu giá trị tuyệt đối 108.
+ Dạng 5. Ứng dụng của Max – Min 113.
§4 – ĐƯỜNG TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ 119.
A Lý thuyết 119.
B Ví dụ minh họa 120.
C Một số dạng toán cơ bản 123.
+ Dạng 1.Cơ bản về tiệm cận của đồ thị hàm số 123.
p Lê Quang Xe i Ô SĐT: 0967.003.131.
MỤC LỤC.
+ Dạng 2.Bài tập tiệm cận của đồ thị hàm số 127.
§5 – CÁC BÀI TOÁN LIÊN QUAN ĐẾN ĐỒ THỊ HÀM SỐ 131.
A Lý thuyết 131.
B Ví dụ minh họa 134.
C Một số dạng toán cơ bản 134.
+ Dạng 1. Đọc và biến đổi đồ thị 134.
+ Dạng 2. Tương giao của đồ thị hàm số 142.
+ Dạng 3. Tiếp tuyến – sự tiếp xúc của hai đồ thị 158.
+ Dạng 4. Toàn tập về phương pháp ghép trục 170.