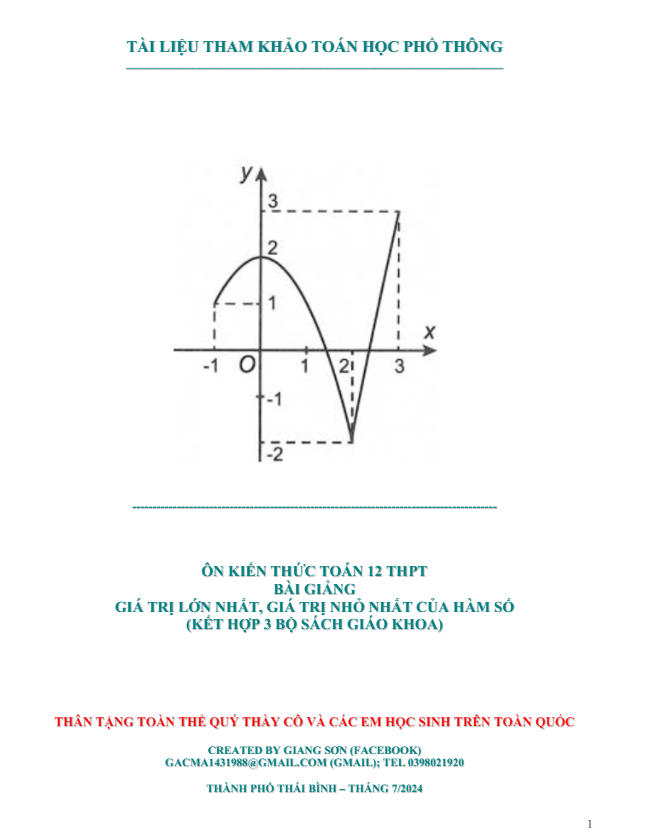Tài liệu gồm 137 trang, tuyển chọn các bài tập trắc nghiệm hàm số (hàm ẩn) vận dụng cao, có đáp án và lời giải chi tiết, giúp học sinh lớp 12 tham khảo khi học chương trình Toán 12 phần Giải tích chương 1: Ứng Dụng Đạo Hàm Để Khảo Sát Và Vẽ Đồ Thị Của Hàm Số.
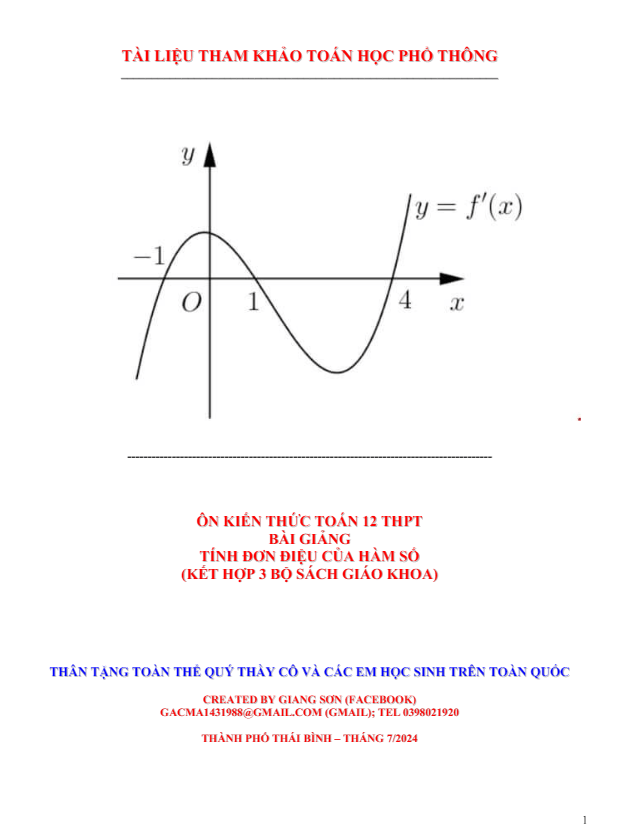
PHẦN 1. SỰ ĐỒNG BIẾN, NGHỊCH BIẾN CỦA HÀM SỐ.
+ Vấn đề 1. Cho đồ thị f'(x). Hỏi khoảng đơn điệu của hàm số f[u(x)].
+ Vấn đề 2. Cho đồ thị f'(x). Hỏi khoảng đơn điệu của hàm số f[u(x)] + g(x).
+ Vấn đề 3. Cho bảng biến thiên f'(x). Hỏi khoảng đơn điệu của hàm số f[u(x)].
+ Vấn đề 4. Cho biểu thức f'(x). Hỏi khoảng đơn điệu của hàm số f[u(x)].
+ Vấn đề 5. Cho biểu thức f'(x;m). Tìm m để hàm số f[u(x)] đồng biến, nghịch biến.
PHẦN 2. CỰC TRỊ CỦA HÀM SỐ.
+ Vấn đề 1. Cho đồ thị f'(x). Hỏi số điểm cực trị của hàm số f[u(x)].
+ Vấn đề 2. Cho biểu thức f'(x). Hỏi số điểm cực trị của hàm số f[u(x)].
+ Vấn đề 3. Cho biểu thức f'(x;m). Tìm m để hàm số f[u(x)] có n điểm cực trị.
+ Vấn đề 4. Cho đồ thị f(x). Hỏi số điểm cực trị của hàm số f[u(x)].
+ Vấn đề 5. Cho bảng biến thiên của hàm f(x). Hỏi số điểm cực trị của hàm f[u(x)].
+ Vấn đề 6. Cho đồ thị f(x). Hỏi số điểm cực trị của hàm số f[u(x;m)].
+ Vấn đề 7. Cho biểu thức f(x;m). Tìm m để hàm số f[u(x)] có n điểm cực trị.
PHẦN 3. GTLN – GTNN CỦA HÀM SỐ.
+ Vấn đề 1. Cho đồ thị hàm số f(x). Hỏi GTLN – GTNN của hàm số f[u(x)] + g(x).
+ Vấn đề 2. Tìm GTLN – GTNN của hàm số f(x), f(|x|), |f(x)|.
+ Vấn đề 3. Cho biết hàm số f(x) đạt GTLN (GTNN) tại x0 thuộc (a;b). Hỏi trên khoảng (c;d) hàm số đạt GTLN (GTNN) tại điểm nào?
+ Vấn đề 4. Bài toán tìm tham số m để GTLN của hàm số đạt GTNN.
+ Vấn đề 5. Cho đồ thị hàm số f'(x). Hỏi GTLN – GTNN của hàm số f[u(x)] + g(x).
PHẦN 4. TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ.
+ Vấn đề 1. Tìm số đường tiệm cận thông qua đồ thị cho trước.
+ Vấn đề 2. Tìm số đường tiệm cận thông qua bảng biến thiên.
+ Vấn đề 3. Tìm số đường tiệm cận thông qua biểu thức của hàm số.
PHẦN 5. TƯƠNG GIAO GIỮA HAI ĐỒ THỊ.
+ Vấn đề 1. Tìm nghiệm của phương trình thông qua biểu thức.
+ Vấn đề 2. Tìm nghiệm của phương trình thông qua bảng biến thiên.
+ Vấn đề 3. Tìm nghiệm của phương trình thông qua đồ thị.