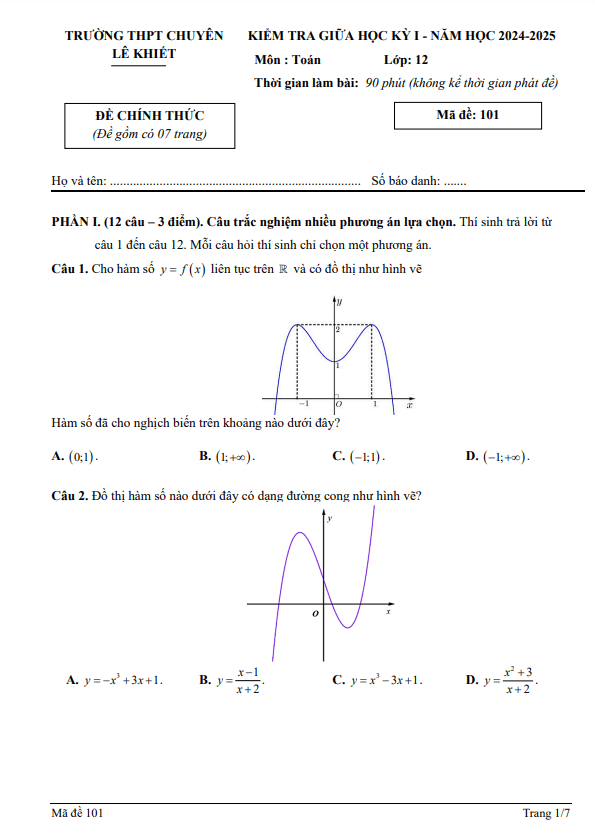
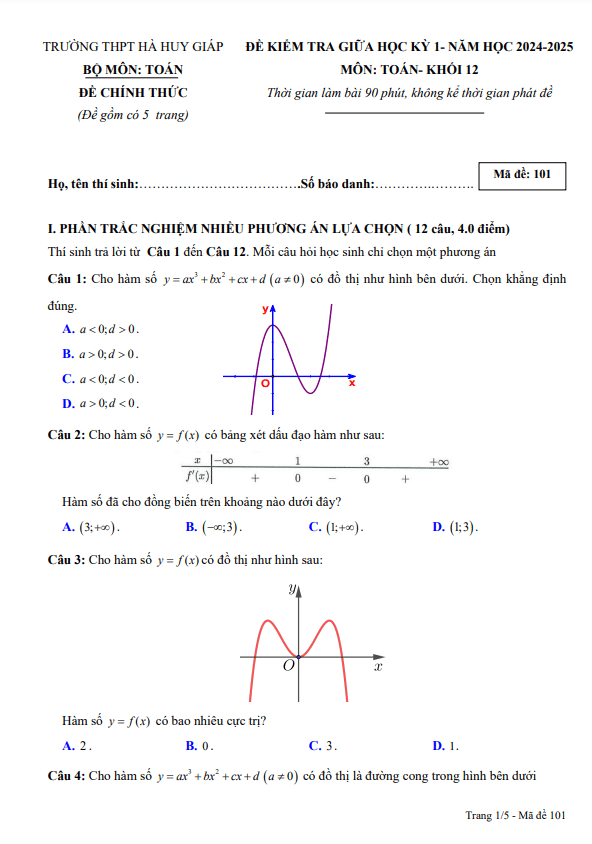
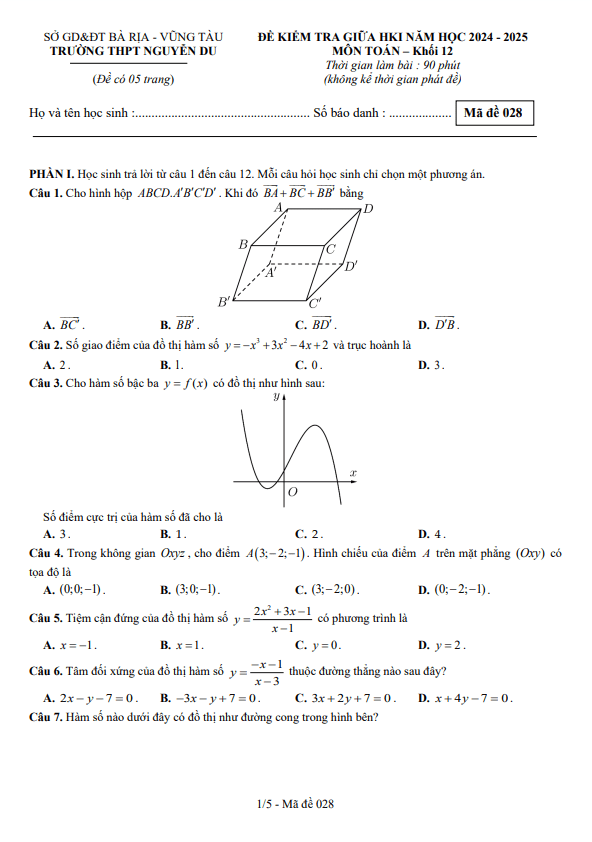
TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra giữa học kỳ 1 môn Toán 12 năm học 2024 – 2025 trường THPT Phan Đình Phùng, thành phố Hà Nội. Đề thi mã đề 101, gồm 06 trang với 12 câu trắc nghiệm nhiều phương án lựa chọn, 04 câu trắc nghiệm đúng / sai, 06 câu trắc nghiệm trả lời ngắn, thời gian làm bài 90 phút.
Trích dẫn Đề giữa học kỳ 1 Toán 12 năm 2024 – 2025 trường THPT Phan Đình Phùng – Hà Nội:
+ Giám đốc của show diễn ca nhạc “ATSH” đang xác định mức giá vé vào cửa cho đêm biểu diễn dự kiến vào tháng 11/2024 tại Hà Nội. Theo kinh nghiệm nhiều năm tổ chức show diễn của mình, giám đốc đã xác định được rằng: Nếu giá vé vào cửa là 85 USD/vé thì trung bình có 15000 khán giả đến xem. Mỗi lần tăng giá vé thêm 10 USD/vé thì số khán giả đến xem sẽ giảm đi 1000 người. Mỗi lần giảm giá vé đi 10 USD/vé thì số khán giả đến xem sẽ tăng lên 1000 người. Biết rằng, trung bình mỗi khán giá đến xem còn giúp show diễn có thêm 5 USD từ các dịch vụ đi kèm và mỗi khán giả vào xem phải có 1 vé vào cửa. Hỏi giám đốc chọn giá vé vào cửa cho show diễn này là bao nhiêu USD/vé để tổng số tiền thu được sau đêm diễn (gồm tổng tiền bán vé và tiền thu từ các dịch vụ đi kèm) là lớn nhất?
+ Cho hàm số f(x) = x3 – 12x + 2 và m là tham số. a) Hàm số y = f(x) có hai điểm cực trị. b) Giá trị lớn nhất của hàm số y = f(x) trên [-2;2] bằng -14. c) Đường thẳng y = 2 cắt đồ thị hàm số y = f(x) tại 3 điểm phân biệt có hoành độ lập thành cấp số cộng. d) Biết giá trị nhỏ nhất của hàm số y = [f(x) + m]2 trên đoạn [-2;2] bằng 1. Khi đó, tổng tất cả các giá trị của tham số m bằng -4.
+ Cho hàm số f(x) = (2x + 1)/(x – 3). a) Hàm số y = f(x) đồng biến trên từng khoảng xác định. b) Tiệm cận đứng của đồ thị hàm số y = f(x) là đường thẳng x = 3. c) Tiệm cận ngang của đồ thị hàm số y = f(x) là đường thẳng y = 3. d) Chu vi hình chữ nhật tạo bởi hai trục tọa độ và hai đường tiệm cận của đồ thị hàm số y = f(x) bằng 10.