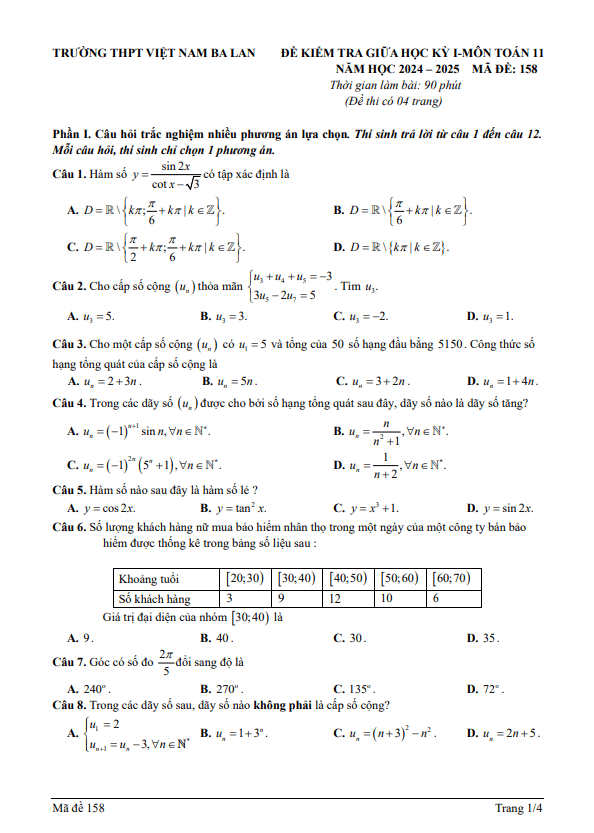TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra giữa học kì 1 môn Toán 11 năm học 2024 – 2025 trường THPT Yên Lạc, tỉnh Vĩnh Phúc. Đề thi được biên soạn theo định dạng trắc nghiệm mới nhất, với cấu trúc gồm 03 phần: trắc nghiệm 04 lựa chọn, câu hỏi đúng sai, câu hỏi điền đáp số; thời gian làm bài 90 phút, có đáp án mã đề 101 102 103 104 105 106 107 108.
Trích dẫn Đề giữa kì 1 Toán 11 năm 2024 – 2025 trường THPT Yên Lạc – Vĩnh Phúc:
+ Một nhà thi đấu có 20 hàng ghế dành cho khán giả. Hàng thứ nhất có 20 ghế, hàng thứ hai có 21 ghế, hàng thứ ba có 22 ghế, …. Cứ như thế, số ghế ở hàng sau nhiều hơn số ghế ở hàng trước là 1 ghế. Trong một giải thi đấu, ban tổ chức đã bán được hết số vé phát ra và số tiền thu được từ bán vé là 76700 nghìn đồng. Biết số vé bán ra bằng số ghế dành cho khán giả của nhà thi đấu và các vé là đồng giá, hỏi giá tiền của mỗi vé là bao nhiêu nghìn đồng?
+ Cho hình vuông ABCD có cạnh bằng 3 và có diện tích S1. Nối 4 trung điểm A1, B1, C1, D1 theo thứ tự của 4 cạnh AB, BC, CD, DA ta được hình vuông thứ hai có diện tích S2. Tiếp tục làm như thế, ta được hình vuông thứ ba là A2B2C2D2 có diện tích S3, … và cứ tiếp tục làm như thế, ta tính được các hình vuông lần lượt có diện tích S4, S5, …, S100. Tính tổng S = S1 + S2 + S3 + … + S100.
+ Số giờ có ánh sáng mặt trời của Thủ đô Hà Nội trong ngày thứ t của một năm không nhuận được cho bởi hàm số d(t) = 3sin[pi/182(t – 70)] + 13 với t thuộc Z và 1 =< t =< 365. Hỏi ngày thứ bao nhiêu trong năm thì số giờ có ánh sáng của Thủ đô Hà Nội đạt lớn nhất?