TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề cương hướng dẫn nội dung ôn tập kiểm tra cuối học kì 1 môn Toán 12 năm học 2024 – 2025 trường THPT Nguyễn Trãi, quận Liên Chiểu, thành phố Đà Nẵng.
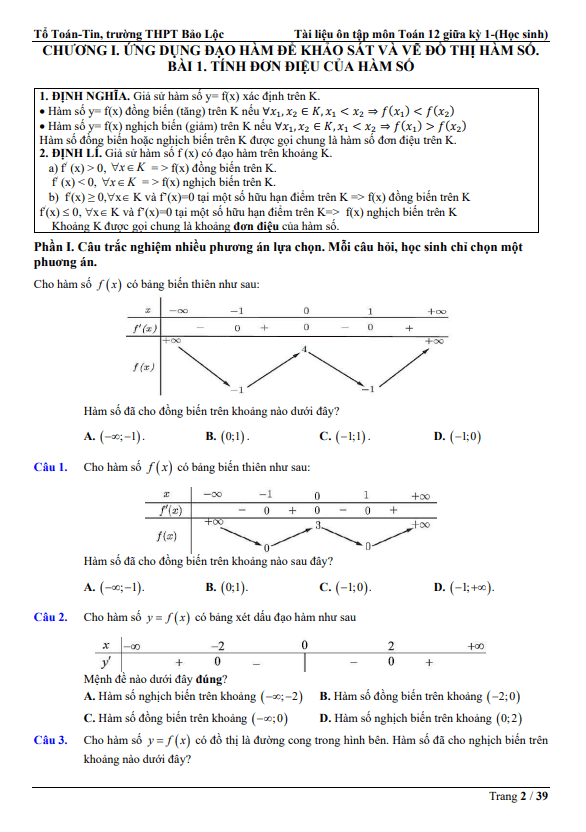
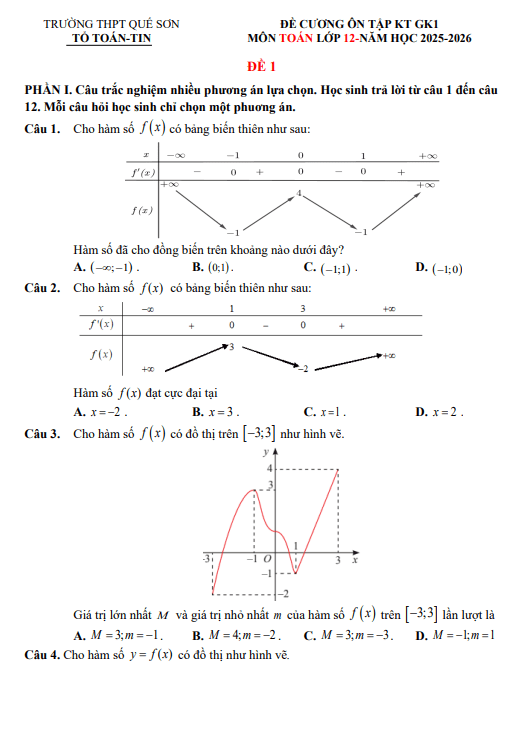
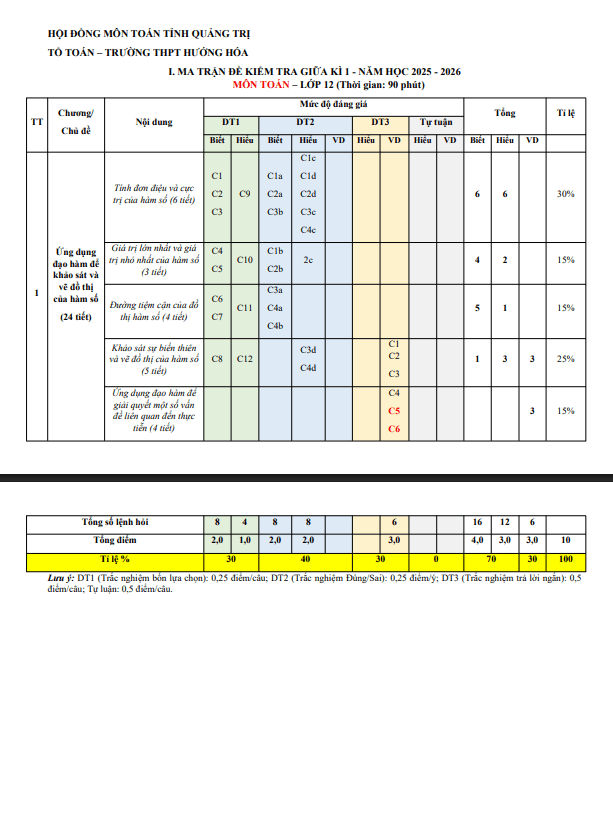
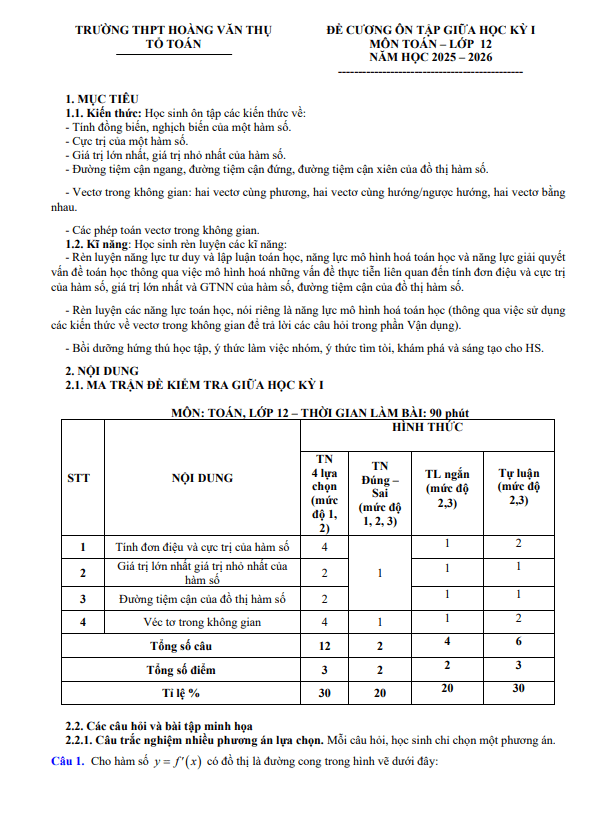
CHƯƠNG I. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ CỦA HÀM SỐ.
– Nhận biết được tính đồng biến, nghịch biến của một hàm số trên một khoảng dựa vào dấu của đạo hàm cấp một của nó.
– Nhận biết được tính đơn điệu, điểm cực trị, giá trị cực trị của hàm số thông qua bảng biến thiên hoặc thông qua hình ảnh hình học của đồ thị hàm số.
– Nhận biết được giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một tập xác định cho trước.
– Thể hiện được tính đồng biến, nghịch biến của hàm số trong bảng biến thiên của hàm số.
– Mô tả được sơ đồ tổng quát để khảo sát hàm số (tìm tập xác định, xét chiều biến thiên, tìm cực trị, tìm tiệm cận, lập bảng biến thiên, vẽ đồ thị).
– Vận dụng được đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn.
CHƯƠNG II. HỆ TRỤC TỌA ĐỘ TRONG KHÔNG GIAN.
– Nhận biết được vectơ và các phép toán vectơ trong không gian (tổng và hiệu của hai vectơ, tích của một số với một vectơ, tích vô hướng của hai vectơ).
– Nhận biết được toạ độ của một vectơ đối với hệ trục toạ độ.
– Xác định được độ dài của một vectơ khi biết toạ độ hai đầu mút của nó và biểu thức toạ độ của các phép toán vectơ.
– Vận dụng được toạ độ của vectơ để giải một số bài toán có liên quan đến thực tiễn.
CHƯƠNG III. CÁC SỐ ĐẶC TRƯNG ĐO MỨC ĐỘ PHÂN TÁN CỦA MẪU SỐ LIỆU GHÉP NHÓM.
– Giải thích được ý nghĩa và vai trò của các số đặc trưng đo mức độ phân tán cho mẫu số liệu ghép nhóm: khoảng biến thiên, khoảng tứ phân vị, phương sai, độ lệch chuẩn trong thực tiễn.
– Chỉ ra được những kết luận nhờ ý nghĩa của các số đặc trưng đo mức độ phân tán cho mẫu số liệu ghép nhóm: khoảng biến thiên, khoảng tứ phân vị, phương sai, độ lệch chuẩn trong trường hợp đơn giản.
– Tính được các số đặc trưng đo mức độ phân tán cho mẫu số liệu ghép nhóm: khoảng biến thiên, khoảng tứ phân vị, phương sai, độ lệch chuẩn.