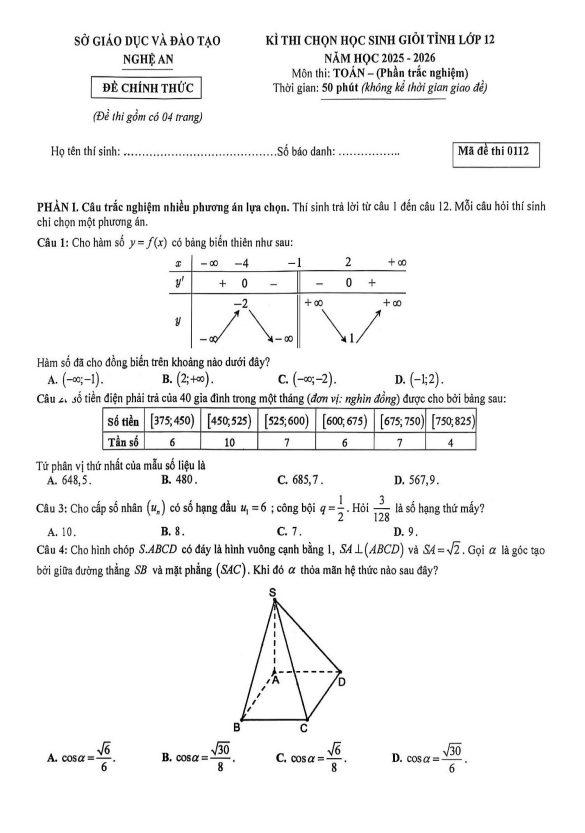
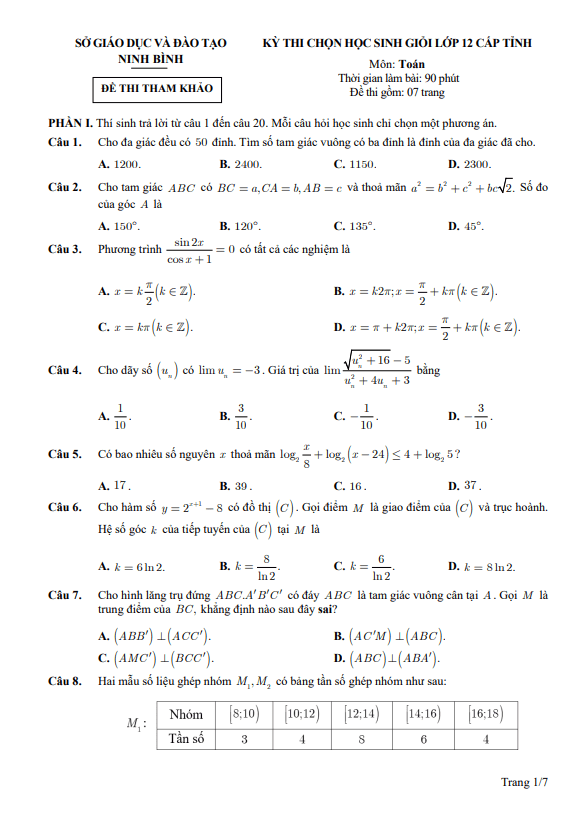TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh đề khảo sát chất lượng đội tuyển học sinh giỏi cấp tỉnh môn Toán 12 THPT lần thứ nhất năm học 2025 – 2026 cụm 09 trường THPT, tỉnh Phú Thọ. Kỳ thi được diễn ra vào ngày 01 tháng 11 năm 2025. Đề thi có đáp án và hướng dẫn chấm điểm.
Trích dẫn Đề khảo sát HSG Toán 12 lần 1 năm 2025 – 2026 cụm 09 trường THPT – Phú Thọ:
+ Hai người tham gia một trò chơi di chuyển theo cạnh của các ô hình vuông như trong hình (hình có 15 x 8 ô hình vuông nhỏ). Người thứ nhất đi từ điểm A đến điểm B, người thứ hai đi từ điểm E đến điểm F. Biết rằng cả hai người cùng đi ngẫu nhiên và theo con đường ngắn nhất. Tính xác suất để cả hai người cùng đi qua điểm I (kết quả làm tròn đến hàng phần nghìn).
+ Trong trận thi đấu bóng bàn đơn nam giữa vận động viên Nguyễn Đức Tuân (người từng đoạt huy chương vàng đơn nam môn bóng bàn tại Seagames 31) với một vận động viên nước ngoài, trận đấu gồm tối đa 5 set (séc), người nào thắng trước 3 set sẽ giành chiến thắng chung cuộc. Xác suất để vận động viên Tuân thắng mỗi set là 0,6. Xác suất để vận động viên Tuân giành chiến thắng trong trận đấu (kết quả làm tròn đến hàng phần trăm) bằng?
+ Cho biết bốn đoạn thẳng nối từ một đỉnh của tứ diện đến trọng tâm mặt đối diện luôn cắt nhau tại một điểm gọi là trọng tâm của tứ diện đó. Một phân tử metan CH4 được cấu tạo bởi bốn nguyên tử hydrogen ở các đỉnh của một tứ diện đều và một nguyên tử carbon ở trọng tâm của tứ diện (tham khảo hình vẽ). Góc liên kết là góc tạo bởi liên kết H–C–H (góc giữa các đường nối nguyên tử carbon với hai trong số các nguyên tử hydrogen). Tính cosin của góc liên kết đó.
File WORD (dành cho quý thầy, cô): TẢI XUỐNG