Bài viết hướng dẫn dùng phương pháp vectơ để giải một số bài toán hình học phẳng, nội dung bài viết gồm hai phần: trình bày phương pháp giải toán và một số ví dụ minh họa có lời giải chi tiết.
Phương pháp giải toán:
1. Phương pháp: Để giải một số bài toán hình học bằng phương pháp vectơ ta tiến hành:
• Bước 1:
+ Lựa chọn một vectơ “gốc”.
+ Chuyển đổi giả thiết, kết luận bài toán từ ngôn ngữ hình học sang ngôn ngữ vectơ.
• Bước 2: Thực hiện các phép biến đổi các biểu thức vectơ theo yêu cầu bài toán.
• Bước 3: Chuyên các kết luận từ ngôn ngữ vectơ sang ngôn ngữ hình học tương ứng.
2. Một số dạng bài toán:
Bài toán 1: Chứng minh ba điểm $A$, $B$, $C$ thẳng hàng.
+ Để chứng minh $A$, $B$, $C$ thẳng hàng ta cần chứng minh $\overrightarrow {AB} $ cùng phương với $\overrightarrow {AC} $ (hoặc $\overrightarrow {AB} $ cùng phương $\overrightarrow {BC} $ hoặc $\overrightarrow {AC} $ cùng phương với $\overrightarrow {BC} $), tức là chứng minh đẳng thức vectơ $\overrightarrow {AB} = k\overrightarrow {AC} $ với $k \in R.$
+ Ngoài ra để chứng minh $A$, $B$, $C$ thẳng hàng ta có thể chứng minh đẳng thức vectơ $\overrightarrow {MB} = k\overrightarrow {MC} + (1 – k)\overrightarrow {MA} $ với $M$ bất kì, $k \in R.$
Bài toán 2: Chứng minh ba đường thẳng $a$, $b$, $c$ đồng quy thì quy về bài toán 1 bằng cách:
+ Gọi $A$ là giao điểm của $a$ và $b.$
+ Chứng minh $A \in c$ tức là $A$, $B$, $C$ thẳng hàng với $B$, $C$ là hai điểm nằm trên đường thẳng $c.$
Bài toán 3: Chứng minh $AB$ song song với $CD$, ta chứng minh $A$, $B$, $C$, $D$ không thẳng hàng và $\overrightarrow {AB} = k\overrightarrow {CD} .$
Bài toán 4: Chứng minh $AB$ vuông góc $CD$, ta chứng minh $\overrightarrow {AB} .\overrightarrow {CD} = 0.$
Bài toán 5: Các dạng toán tính độ dài, tính góc thì chú ý sử dụng:
$AB = \sqrt {\left| {{{\overrightarrow {AB} }^2}} \right|} = \sqrt {\overrightarrow {AB} .\overrightarrow {AB} } $
$\cos \alpha = \frac{{\vec a.\vec b}}{{\left| {\vec a} \right|.\left| {\vec b} \right|}}$ ($\alpha $ là góc giữa hai vectơ $\overrightarrow a $, $\overrightarrow b $).
Ví dụ minh họa:
Bài toán 1: Cho tam giác $ABC$, lấy các điểm $M$, $N$, $P$ sao cho:
$\overrightarrow {MB} – 2\overrightarrow {MC} $ $ = \overrightarrow {NA} + 2\overrightarrow {NC} $ $ = \overrightarrow {PA} + \overrightarrow {PB} = \vec 0.$
Chứng minh rằng $M$, $N$, $P$ thẳng hàng.

Để chứng minh $M$, $N$, $P$ thẳng hàng ta cần chứng minh $\overrightarrow {PM} = k\overrightarrow {PN} $, $k \in R.$
Biểu thị $\overrightarrow {PM} $, $\overrightarrow {PN} $ theo hai vectơ $\overrightarrow {AB} $, $\overrightarrow {AC} $ (hệ vectơ “gốc”).
Ta có:
$\overrightarrow {PN} = \overrightarrow {PA} + \overrightarrow {AN} $ $ = – \frac{1}{2}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} .$
$\overrightarrow {PM} = \overrightarrow {PB} + \overrightarrow {BM} $ $ = \frac{1}{2}\overrightarrow {AB} + 2\overrightarrow {BC} $ $ = \frac{1}{2}\overrightarrow {AB} + 2(\overrightarrow {AC} – \overrightarrow {AB} )$ $ = – \frac{3}{2}\overrightarrow {AB} + 2\overrightarrow {AC} $ $ = 3\left( { – \frac{1}{2}\overrightarrow {AB} + \frac{2}{3}\overrightarrow {AC} } \right) = 3\overrightarrow {PN} .$
Vậy $\overrightarrow {PM} = 3\overrightarrow {PN} $ hay $M$, $N$, $P$ thẳng hàng.
Bài toán 2: Cho tam giác $ABC$, gọi $O$, $G$, $H$ lần lượt là tâm đường tròn ngoại tiếp, trọng tâm, trực tâm của tam giác $ABC.$ Chứng minh rằng $O$, $G$, $H$ thẳng hàng.

Để chứng minh $O$, $G$, $H$ thẳng hàng, ta cần chứng minh $\overrightarrow {OG} = k\overrightarrow {OH} $, $k \in R.$
Ta có: $\overrightarrow {OG} = \frac{1}{3}(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} ).$
Gọi $D$ là điểm đối xứng với $A$ qua $O$, $E$ là trung điểm của $BC.$
Ta có:
$CD//BH$ vì cùng vuông góc với $AC.$
$BD//CH$ vì cùng vuông góc với $AB.$
Suy ra $BDCH$ là hình bình hành. Do đó $E$ là trung điểm của $HD.$
Do đó: $\overrightarrow {OH} = \overrightarrow {OA} + \overrightarrow {AH} $ $ = \overrightarrow {OA} + 2\overrightarrow {OE} $ $ = \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} .$
Như vậy $\overrightarrow {OG} = \frac{1}{3}\overrightarrow {OH} $ hay $O$, $G$, $H$ thẳng hàng.
Bài toán 3: Cho hai hình bình hành $ABCD$ và ${A_1}{B_1}{C_1}{D_1}$ sắp xếp sao cho ${B_1}$ thuộc cạnh $AB$, ${D_1}$ thuộc cạnh $AD.$ Chứng minh rằng các đường thẳng $D{B_1}$, $B{D_1}$ và $C{C_1}$ đồng quy.
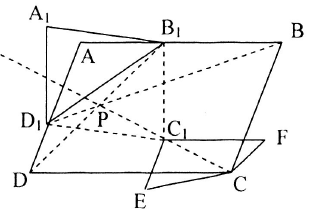
Gọi $\overrightarrow {AB} = \vec a$, $\overrightarrow {AD} = \vec b.$
Vì $A$, $B_1$, $B$ thẳng hàng nên: $\overrightarrow {A{B_1}} = k\overrightarrow {AB} $ $(1).$
Vì $A$, $D_1$, $D$ thẳng hàng nên: ${\overrightarrow {AD} _1} = h\overrightarrow {AD} $ $(2).$
Gọi $P$ là giao điểm $D{B_1}$ và ${D_1}B.$
Vì $B_1$, $P$, $D$ thẳng hàng nên $\overrightarrow {AP} = \alpha \overrightarrow {A{B_1}} + (1 – \alpha )\overrightarrow {AD} $ $(3).$
Vì $B$, $P$, $D_1$ thẳng hàng nên $\overrightarrow {AP} = \beta \overrightarrow {AB} + (1 – \beta )\overrightarrow {A{D_1}} $ $(4).$
Từ $(1)$ và $(3)$ suy ra $\overrightarrow {AP} = \alpha k\vec a + (1 – \alpha )\vec b.$
Từ $(2)$ và $(4)$ suy ra $\overrightarrow {AP} = \beta \overrightarrow a + (1 – \beta )h\overrightarrow b .$
Vì $\overrightarrow a $ và $\overrightarrow b $ không cùng phương nên ta suy ra được $\left\{ {\begin{array}{*{20}{l}}
{\alpha k = \beta }\\
{1 – \alpha = (1 – \beta )h}
\end{array}} \right.$
Suy ra: $\alpha = \frac{{1 – h}}{{1 – kh}}.$
Vậy $\overrightarrow {AP} = \frac{{k(1 – h)}}{{1 – kh}}\vec a + \frac{{h(1 – k)}}{{1 – kh}}\vec b.$
Ta lại có: $\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} = \vec a + \vec b.$
Từ đó suy ra $\overrightarrow {PC} = \overrightarrow {AC} – \overrightarrow {AP} $ $ = \frac{{1 – k}}{{1 – kh}}\overrightarrow a + \frac{{1 – h}}{{1 – kh}}\overrightarrow b .$
Hơn nữa: $\overrightarrow {{D_1}D} = (1 – h)\vec b = \overrightarrow {{C_1}E} $, $\overrightarrow {{B_1}B} = (1 – k)\overrightarrow a = \overrightarrow {{C_1}F} .$
Suy ra: $\overrightarrow {{C_1}C} = \overrightarrow {{C_1}E} + \overrightarrow {{C_1}F} $ $ = (1 – k)\overrightarrow a + (1 – h)\overrightarrow b .$
Vậy $\overrightarrow {{C_1}C} = (1 – kh)\overrightarrow {PC} .$ Hay $C_1$, $C$, $P$ thẳng hàng tức là ${C_1}C$ đi qua $P.$
Do vậy $D{B_1}$, ${D_1}B$ và $C{C_1}$ đồng quy tại $P.$
Bài toán 4: Cho tứ giác $ABCD$ và điểm $M.$ Gọi $N$, $P$, $Q$, $R$ lần lượt là các điểm đối xứng của $M$ qua trung điểm của các cạnh của tứ giác. Chứng minh rằng $MPQR$ là hình bình hành.
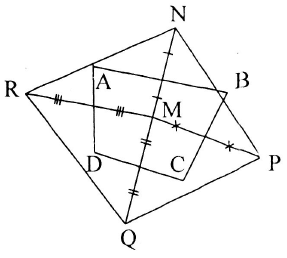
Ta có:
$\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MN} .$
$\overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow {MP} .$
$\overrightarrow {MC} + \overrightarrow {MD} = \overrightarrow {MQ} .$
$\overrightarrow {MD} + \overrightarrow {MA} = \overrightarrow {MR} .$
Từ đó suy ra:
$\overrightarrow {RN} = \overrightarrow {MN} – \overrightarrow {MR} $ $ = \overrightarrow {MA} + \overrightarrow {MB} – \overrightarrow {MD} – \overrightarrow {MA} $ $ = \overrightarrow {MB} – \overrightarrow {MD} = \overrightarrow {DB} .$
$\overrightarrow {QP} = \overrightarrow {MP} – \overrightarrow {MQ} $ $ = \overrightarrow {MB} + \overrightarrow {MC} – \overrightarrow {MC} – \overrightarrow {MD} $ $ = \overrightarrow {MB} – \overrightarrow {MD} = \overrightarrow {DB} .$
Vậy $\overrightarrow {RN} = \overrightarrow {QP} .$ Do đó $NPRQ$ là hình bình hành.
Bài toán 5: Cho tam giác $ABC$ cân tại $A$ và $D$ là trung điểm của cạnh $BC.$ $H$ là hình chiếu vuông góc của $D$ trên cạnh $AC$ và $I$ là trung điểm của đoạn $DH.$ Chứng minh rằng $AI \bot BH.$
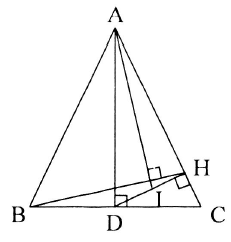
Ta có: $\overrightarrow {AI} .\overrightarrow {BH} $ $ = \frac{1}{2}(\overrightarrow {AD} + \overrightarrow {AH} ).(\overrightarrow {BD} + \overrightarrow {DH} )$ $ = \quad \frac{1}{2}(\overrightarrow {AD} .\overrightarrow {BD} + \overrightarrow {AH} .\overrightarrow {BD} + \overrightarrow {AD} .\overrightarrow {DH} + \overrightarrow {AH} .\overrightarrow {DH} )$ $ = \frac{1}{2}(\overrightarrow {AH} .\overrightarrow {BD} + \overrightarrow {AD} .\overrightarrow {DH} )$ (vì $AD \bot BD$ và $AH \bot DH$ nên $\overrightarrow {AD} .\overrightarrow {BD} = \overrightarrow {AH} .\overrightarrow {DH} = 0$) $ = \frac{1}{2}\left[ {(\overrightarrow {AD} + \overrightarrow {DH} )\overrightarrow {DC} + \overrightarrow {AD} .\overrightarrow {DH} } \right]$ $ = \frac{1}{2}(\overrightarrow {DH} .\overrightarrow {DC} + \overrightarrow {DH} .\overrightarrow {AD} )$ $ = \frac{1}{2}\overrightarrow {DH} (\overrightarrow {AD} + \overrightarrow {DC} )$ $ = \frac{1}{2}\overrightarrow {DH} .\overrightarrow {AC} = 0.$
Vậy $\overrightarrow {AI} .\overrightarrow {BH} = 0$, do đó $AI \bot BH.$
Bài toán 6: Cho tứ giác $ABCD.$ Hai đường chéo cắt nhau tại $O.$ Gọi $H$, $K$ lần lượt là trực tâm của tam giác $ABO$ và tam giác $CDO.$ $I$, $J$ là trung điểm của $AD$ và $BC.$ Chứng minh rằng $HK \bot IJ.$

Ta có:
$\overrightarrow {IJ} = \overrightarrow {IA} + \overrightarrow {AB} + \overrightarrow {BJ} .$
$\overrightarrow {IJ} = \overrightarrow {ID} + \overrightarrow {DC} + \overrightarrow {CJ} .$
Suy ra: $\overrightarrow {IJ} = \frac{1}{2}(\overrightarrow {AB} + \overrightarrow {DC} ).$
Khi đó: $\overrightarrow {HK} .\overrightarrow {IJ} = \frac{1}{2}(\overrightarrow {OK} – \overrightarrow {OH} )(\overrightarrow {AB} + \overrightarrow {DC} )$ $ = \frac{1}{2}(\overrightarrow {OK} .\overrightarrow {AB} + \overrightarrow {OK} .\overrightarrow {DC} – \overrightarrow {OH} .\overrightarrow {AB} – \overrightarrow {OH} .\overrightarrow {DC} )$ $ = \frac{1}{2}(\overrightarrow {OK} .\overrightarrow {AB} – \overrightarrow {OH} .\overrightarrow {DC} )$ $ = \frac{1}{2}\left[ {(\overrightarrow {OC} + \overrightarrow {CK} )(\overrightarrow {OB} – \overrightarrow {OA} ) – (\overrightarrow {OA} + \overrightarrow {AH} )(\overrightarrow {OC} – \overrightarrow {OD} )} \right]$ $ = \frac{1}{2}\left[ {(\overrightarrow {OB} – \overrightarrow {OA} – \overrightarrow {AH} )\overrightarrow {OC} – (\overrightarrow {CK} + \overrightarrow {OC} – \overrightarrow {OD} )\overrightarrow {OA} } \right]$ $ = \frac{1}{2}\left[ {(\overrightarrow {HA} + \overrightarrow {AO} + \overrightarrow {OB} )\overrightarrow {OC} – (\overrightarrow {DO} + \overrightarrow {OC} + \overrightarrow {CK} )\overrightarrow {OA} } \right]$ $ = \frac{1}{2}(\overrightarrow {HB} .\overrightarrow {OC} – \overrightarrow {DK} .\overrightarrow {OA} ) = 0.$
Vậy $HK \bot IJ.$
Bài toán 7: Cho tam giác $ABC$ và đường phân giác trong $AD.$ Gọi $H$ là hình chiếu của $D$ lên $AB$, $K$ là hình chiếu của $D$ lên $AC.$ Biết $\overrightarrow {AB} .\overrightarrow {AD} = 2{a^2}$, $\overrightarrow {AC} .\overrightarrow {AD} = 3{a^2}$, $AH = a.$
a) Tính $AB$, $AC.$
b) Tính $\overrightarrow {AB} .\overrightarrow {AC} $ và cosin của góc giữa hai đường thẳng $AB$, $AC.$
c) Tính $AD$ và $BC.$
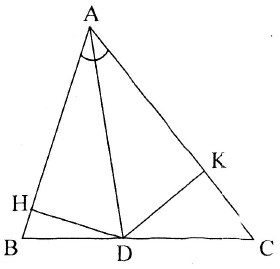
a) Ta có:
$\overrightarrow {AB} .\overrightarrow {AD} = AB.AH = 2{a^2}.$
Suy ra: $AB = 2a.$
$\overrightarrow {AC} .\overrightarrow {AD} = AC.AK$ $ = AC.AH = 3{a^2}$ (vì $AK = AH$).
Suy ra: $AC = 3a.$
b) $\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}} = \frac{2}{3}.$
Suy ra: $3\overrightarrow {DB} + 2\overrightarrow {DC} = \vec 0$ $ \Rightarrow 3(\overrightarrow {AB} – \overrightarrow {AD} ) + 2(\overrightarrow {AC} – \overrightarrow {AD} ) = \vec 0$ $ \Rightarrow 3\overrightarrow {AB} + 2\overrightarrow {AC} = 5\overrightarrow {AD} $ $ \Rightarrow 3\overrightarrow {AB} .\overrightarrow {AC} + 2{\overrightarrow {AC} ^2} = 5\overrightarrow {AD} .\overrightarrow {AC} $ $ \Rightarrow 3\overrightarrow {AB} .\overrightarrow {AC} = 5\overrightarrow {AD} .\overrightarrow {AC} – 2{\overrightarrow {AC} ^2}$ $ \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = \frac{{15{a^2} – 18{a^2}}}{3} = – {a^2}.$
Gọi $\alpha $ là góc giữa $AB$ và $AC$, ta có: $\cos \alpha = \left| {\cos (\overrightarrow {AB} ,\overrightarrow {AC} )} \right|$ $ = \frac{{\left| {\overrightarrow {AB} .\overrightarrow {AC} } \right|}}{{AB.AC}} = \frac{{{a^2}}}{{2a.3a}} = \frac{1}{6}.$
c) Vì $3\overrightarrow {AB} + 2\overrightarrow {AC} = 5\overrightarrow {AD} .$
Suy ra $25A{D^2} = 9A{B^2} + 4A{C^2} + 12\overrightarrow {AB} .\overrightarrow {AC} $ $ = 36{a^2} + 36{a^2} – 12{a^2}$ $ = 60{a^2}.$
Vậy $AD = \frac{{2a\sqrt {15} }}{5}.$
$B{C^2} = {\overrightarrow {BC} ^2} = {(\overrightarrow {AC} – \overrightarrow {AB} )^2}$ $ = A{C^2} + A{B^2} – 2\overrightarrow {AB} .\overrightarrow {AC} $ $ = 9{a^2} + 4{a^2} + 2{a^2} = 15{a^2}.$
Vậy $BC = a\sqrt {15} .$









