Bài viết hướng dẫn một số phương pháp giải phương trình lượng giác bậc cao đối với một hàm số lượng giác.
I. PHƯƠNG PHÁP
Bài toán: Giải phương trình bậc cao đối với một hàm số lượng giác.
PHƯƠNG PHÁP CHUNG:
1. Đối với phương trình bậc $3$: $a{t^3} + b{t^2} + ct + d = 0$ $(1).$
Ta lựa chọn một trong ba hướng:
+ Hướng 1: Nếu xác định được nghiệm ${t_0}$ thì:
$(1) \Leftrightarrow \left( {t – {t_0}} \right)\left( {a{t^2} + Bt + C} \right) = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t = {t_0}}\\
{a{t^2} + Bt + C = 0\:\left( 2 \right)}
\end{array}} \right..$
Khi đó việc giải $(1)$ được dẫn về việc giải $(2).$
+ Hướng 2: Sử dụng phương pháp hằng số biến thiên.
+ Hướng 3: Sử dụng phương pháp hàm số đồ thị.
2. Đối với phương trình bậc $4$: $a{t^4} + b{t^3} + c{t^2} + dt + e = 0$ $(3).$
Ta lựa chọn một trong bốn hướng:
+ Hướng 1: Nếu xác định được nghiệm ${t_0}$ thì:
$(3) \Leftrightarrow $ $\left( {t – {t_0}} \right)\left( {a{t^3} + B{t^2} + Ct + D} \right) = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t = {t_0}}\\
{a{t^3} + B{t^2} + Ct + D = 0\:(4)}
\end{array}} \right..$
Khi đó việc giải $(3)$ được dẫn về việc giải $(4).$
+ Hướng 2: Sử dụng phương pháp đặt ẩn phụ.
+ Hướng 3: Sử dụng phương pháp hằng số biến thiên.
+ Hướng 4: Sử dụng phương pháp hàm số đồ thị.
Ví dụ 1: (Đại học Thái Nguyên – 1997): Giải phương trình:
$4{\cos ^2}x – \cos 3x$ $ = 6\cos x + 2(1 + \cos 2x).$
Biến đổi phương trình về dạng:
$4{\cos ^2}x – \left( {4{{\cos }^3}x – 3\cos x} \right)$ $ = 6\cos x + 4{\cos ^2}x.$
$ \Leftrightarrow 4{\cos ^3}x + 3\cos x = 0$ $ \Leftrightarrow \left( {4{{\cos }^2}x + 3} \right)\cos x = 0.$
$ \Leftrightarrow \cos x = 0$ $ \Leftrightarrow x = \frac{\pi }{2} + k\pi $, $k \in Z.$
Vậy phương trình có một họ nghiệm.
Ví dụ 2: Cho phương trình: $\cos 3x – \cos 2x + m\cos x – 1 = 0$ $(1).$
a. Giải phương trình với $m = 1.$
b. (ĐH Y Dược TP HCM – 1999): Tìm $m$ để phương trình có đúng $7$ nghiệm thuộc khoảng $\left( { – \frac{\pi }{2},2\pi } \right).$
Biến đổi phương trình về dạng:
$4{\cos ^3}x – 3\cos x$ $ – \left( {2{{\cos }^2}x – 1} \right) + m\cos x – 1 = 0$ $ \Leftrightarrow 4{\cos ^3}x – 2{\cos ^2}x$ $ + (m – 3)\cos x = 0.$
Đặt $t = \cos x$, điều kiện $|t| \le 1$, phương trình có dạng:
$4{t^3} – 2{t^2} + (m – 3)t = 0$ $ \Leftrightarrow \left( {4{t^2} – 2t + m – 3} \right)t = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t = 0}\\
{4{t^2} – 2t + m – 3 = 0\:\left( 2 \right)}
\end{array}} \right..$
Với $t = 0$:
$ \Leftrightarrow \cos x = 0$ $ \Leftrightarrow x = \frac{\pi }{2} + k\pi $ $(*).$
a. Với $m = 1$, ta được:
$(2) \Leftrightarrow 4{t^2} – 2t – 2 = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t = 1}\\
{t = – \frac{1}{2}}
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\cos x = 1}\\
{\cos x = – \frac{1}{2}}
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 2k\pi }\\
{x = \pm \frac{{2\pi }}{3} + 2k\pi }
\end{array}} \right.$, $k \in Z.$
Vậy với $m = 1$ phương trình có $4$ họ nghiệm.
b. Trước hết ta tìm các nghiệm thoả mãn điều kiện đầu bài từ $(*)$, ta được:
$\left[ {\begin{array}{*{20}{l}}
{{x_1} = \frac{\pi }{2}}\\
{{x_2} = \frac{{3\pi }}{2}}
\end{array}} \right..$
Vậy để phương trình $(1)$ có đúng $7$ nghiệm thuộc $\left( { – \frac{\pi }{2},2\pi } \right).$
$\Leftrightarrow$ phương trình $(2)$ có nghiệm thoả mãn: $ – 1 < {t_1} < 0 < {t_2} < 1.$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{af( – 1) > 0}\\
{af(0) < 0}\\
{af(1) > 0}
\end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{m + 3 > 0}\\
{m – 3 < 0}\\
{m – 1 > 0}
\end{array}} \right.$ $ \Leftrightarrow 1 < m < 3.$
Vậy với $1<m< 3$ thoả mãn điều kiện đầu bài.
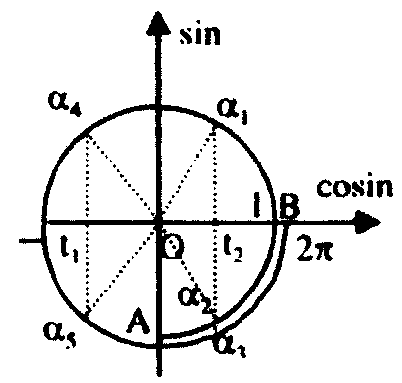
Chú ý: Để các em học sinh tiện theo dõi ta có thể lý giải điều kiện trên có được bởi:
1. Với ${t_2} \in (0,1)$ thì bằng cách dựng đường thẳng qua ${t_2}$ vuông góc với trục cosin ta được ba nghiệm ${\alpha _1}$, ${\alpha _2}$ và ${\alpha _3}$ thuộc cung $\widehat {AB}.$
2. Với ${t_1} \in ( – 1,0)$ thì bằng cách dựng đường thẳng qua ${t_1}$ vuông góc với trục cosin ta được hai nghiệm ${\alpha _4}$ và ${\alpha _5}$ thuộc cung $\widehat {AB}.$
Ví dụ 3: Cho phương trình:
${\cot ^3}x – 3{\cot ^2}x + m = 0$ $(1).$
a. Với $m = -1$, phương trình có mấy nghiệm thuộc $\left( {0,\frac{\pi }{2}} \right)$?
b. Tìm $m$ để phương trình có ba nghiệm phân biệt thuộc $(0,\pi ).$
Điều kiện:
$\sin x \ne 0 \Leftrightarrow x \ne k\pi $, $k \in Z.$
Đặt $\cot x = t$, khi đó phương trình có dạng:
${t^3} – 3{t^2} + m = 0.$
Nghiệm của phương trình $(1)$ là hoành độ giao điểm của đồ thị hàm số $y = {t^3} – 3{t^2}$ với đường thẳng $y =-m.$
Xét hàm số $y = {x^3} – 3{x^2}$ trên $R.$
Đạo hàm:
$y’ = 3{t^2} – 6t$, $y’ = 0$ $ \Leftrightarrow 3{t^2} – 6t = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t = 0}\\
{t = 2}
\end{array}} \right..$
Bảng biến thiên:

a. Với $m = – 1$, đường thẳng $y = 1$ cắt đồ thị hàm số tại một điểm có hoành độ ${t_1} > 2$, suy ra phương trình $(1)$ nghiệm duy nhất thuộc $\left( {0,\frac{\pi }{2}} \right).$
b. Để phương trình có ba nghiệm phân biệt thuộc $(0,\pi )$ điều kiện là:
$ – 4 < – m < 0$ $ \Leftrightarrow 0 < m < 4.$
Ví dụ 4: Cho phương trình:
${\tan ^4}x + \left( {2m – 1} \right){\tan ^3}x$ $ + \left( {{m^2} – 2m} \right){\tan ^2}x – \left( {{m^2} – m + 1} \right)\tan x$ $ – m + 1 = 0$ $(1).$
a. Giải phương trình với $m = -1.$
b. Xác định $m$ để phương trình có $4$ nghiệm phân biệt thuộc $\left( { – \frac{\pi }{2},\frac{\pi }{2}} \right).$
Điều kiện:
$\cos x \ne 0$ $ \Leftrightarrow x \ne \frac{\pi }{2} + k\pi $, $k \in Z.$
Đặt $\tan x = t$, khi đó phương trình có dạng:
${t^4} + (2m – 1){t^3} + \left( {{m^2} – 2m} \right){t^2}$ $ – \left( {{m^2} – m + 1} \right)t – m + 1 = 0.$
$ \Leftrightarrow (t – 1)\left( {{t^3} + 2m{t^2} + {m^2}t + m – 1} \right) = 0.$
$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t – 1 = 0}\\
{{t^3} + 2m{t^2} + {m^2}t + m – 1 = 0}
\end{array}} \right.$ $(I).$
Để tiếp tục phân tích $(2)$, ta viết lại $(2)$ dưới dạng:
$t{m^2} + \left( {2{t^2} + 1} \right)m + {t^3} – 1 = 0.$
Coi $m$ là ẩn, còn $t$ là tham số, ta được phương trình bậc $2$ theo $m$ và giải ra ta được:
$\left[ {\begin{array}{*{20}{l}}
{m = 1 – t}\\
{m = – \frac{{{t^2} + t + 1}}{t}}
\end{array}} \right..$
Do đó $(2)$ được chuyển về dạng:
$(t + m – 1)\left[ {{t^2} + (m + 1)t + 1} \right] = 0.$
Khi đó:
$(I) \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t – 1 = 0}\\
{t + m – 1 = 0}\\
{g(t) = {t^2} + (m + 1)t + 1 = 0\:\left( 3 \right)}
\end{array}} \right.$ $(II).$
a. Với $m = -1:$
$(II) \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t – 1 = 0}\\
{t – 2 = 0}\\
{{t^2} + 1 = 0}
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t = 1}\\
{t = 2}
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\tan x = 1}\\
{\tan x = 2 = \tan \alpha }
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \frac{\pi }{4} + k\pi }\\
{x = \alpha + k\pi }
\end{array}} \right.$, $k \in Z.$
Vậy phương trình có hai họ nghiệm.
b. Để phương trình có $4$ nghiệm phân biệt $x \in \left( { – \frac{\pi }{2},\frac{\pi }{2}} \right).$
$ \Leftrightarrow (3)$ có $2$ nghiệm phân biệt khác $1$ và $1- m$ và $1 – m \ne 1.$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\Delta {‘_g} > 0}\\
{g(1) \ne 0}\\
{g(1 – m) \ne 0}\\
{1 – m \ne 1}
\end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{{m^2} + 2m – 3 > 0}\\
{m + 3 \ne 0}\\
{3 – 2m \ne 0}\\
{m \ne 0}
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{1 < m \ne \frac{3}{2}}\\
{m < – 3}
\end{array}} \right..$
Vậy với $m \in ( – \infty , – 3) \cup (1, + \infty )\backslash \left\{ {\frac{3}{2}} \right\}$ phương trình có $4$ nghiệm phân biệt.
II. CÁC BÀI TOÁN THI
Bài 1: (ĐHNN – 2000): Giải phương trình:
$2\cos 2x – 8\cos x + 7 = \frac{1}{{\cos x}}.$
Điều kiện:
$\cos x \ne 0$ $ \Leftrightarrow x \ne \frac{\pi }{2} + k\pi $, $k \in Z.$
Biến đổi phương trình về dạng:
$\left[ {2\left( {2{{\cos }^2}x – 1} \right) – 8\cos x + 7} \right]\cos x = 1$ $ \Leftrightarrow 4{\cos ^3}x – 8{\cos ^2}x + 5\cos x – 1 = 0.$
Đặt $t=\cos x$, điều kiện $|t| \le 1.$
Khi đó phương trình có dạng:
$4{t^3} – 8{t^2} + 5t – 1 = 0$ $ \Leftrightarrow (t – 1)\left( {4{t^2} – 4t + 1} \right) = 0$ $ \Leftrightarrow (t – 1){(2t – 1)^2} = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{t = 1}\\
{t = \frac{1}{2}}
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\cos x = 1}\\
{\cos x = \frac{1}{2}}
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 2k\pi }\\
{x = \pm \frac{\pi }{3} + 2k\pi }
\end{array}} \right.$, $k \in Z.$
Vậy phương trình có ba họ nghiệm.
Bài 2: (ĐHQG TP HCM khối D – 1999): Cho phương trình:
$(\cos x + 1)(\cos 2x – m\cos x) = m{\sin ^2}x$ $(1).$
a. Giải phương trình với $m = -2.$
b. Tìm $m$ để phương trình có đúng $2$ nghiệm thuộc $\left[ {0,\frac{{2\pi }}{3}} \right].$
Biến đổi phương trình về dạng:
$(\cos x + 1)(\cos 2x – m\cos x)$ $ = m\left( {1 – {{\cos }^2}x} \right).$
$ \Leftrightarrow (\cos x + 1)[\cos 2x – m\cos x – m(1 – \cos x)] = 0.$
$ \Leftrightarrow (\cos x + 1)(\cos 2x – m) = 0.$
$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\cos x = – 1}\\
{\cos 2x = m}
\end{array}} \right.$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = \pi + 2k\pi }\\
{\cos 2x = m\:\left( * \right)}
\end{array}} \right.$, $k \in Z.$
a. Với $m = -2$, phương trình $(*)$ vô nghiệm.
Vậy với $m = -2$, phương trình có một họ nghiệm $x = \pi + 2k\pi $, $k \in Z.$
b. Để phương trình có đúng $2$ nghiệm thuộc $\left[ {0,\frac{{2\pi }}{3}} \right].$
$ \Leftrightarrow $ phương trình $\cos t = m$ (với $t = 2x$) có đúng $2$ nghiệm thuộc $\left[ {0,\frac{{4\pi }}{3}} \right].$
$ \Leftrightarrow – 1 < m \le – \frac{1}{2}.$
Vậy với $ – 1 < m \le – \frac{1}{2}$ thoả mãn điều kiện đầu bài.
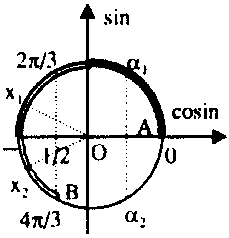
Chú ý: Để các em học sinh tiện theo dõi ta có thể lý giải điều kiện trên có được bởi:
+ Nếu $ – \frac{1}{2} < m \le 1$ thì bằng cách dựng đường thẳng vuông góc với trục cosin ta được hai nghiệm ${\alpha _1}$ và ${\alpha _2}$ nhưng khi đó dễ thấy ${\alpha _2}$ không thuộc cung $\widehat {AB}$, tức là chỉ có $1$ nghiệm được chấp nhận.
Nếu $ – 1 < m \le – \frac{1}{2}$ thì bằng cách dựng đường thẳng vuông góc với trục cosin ta được hai nghiệm ${x_1}$, ${x_2}$ và cả hai nghiệm này đều thuộc cung $\widehat {AB}$, tức là có $2$ nghiệm được chấp nhận.
Bài 3: (ĐHSP TPHCM khối A – 2000): Cho phương trình:
$\sin 3x – m\cos 2x – (m + 1)\sin x + m = 0.$
Tìm $m$ để phương trình có đúng $8$ nghiệm thuộc $(0,3\pi ).$
Biến đổi phương trình về dạng:
$3\sin x – 4{\sin ^3}x – m\left( {1 – 2{{\sin }^2}x} \right)$ $ – (m + 1)\sin x + m = 0.$
$ \Leftrightarrow \left( {4{{\sin }^2}x – 2m\sin x + m – 2} \right)\sin x = 0.$
$ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{\sin x = 0}\\
{4{{\sin }^2}x – 2m\sin x + m – 2 = 0\:\left( 1 \right)}
\end{array}} \right..$
+ Với $\sin x = 0$:
$ \Leftrightarrow x = k\pi $ $\mathop \Leftrightarrow \limits^{x \in (0,3\pi )} \left[ {\begin{array}{*{20}{l}}
{{x_1} = \pi }\\
{{x_2} = 2\pi }
\end{array}} \right..$
+ Với phương trình $(1)$, đặt $t = \sin x$, điều kiện $|t| \le 1$, ta được:
$4{t^2} – 2mt + m – 2 = 0$ $(2).$
Vậy để phương trình có đúng $8$ nghiệm thuộc $(0,3\pi ).$
$ \Leftrightarrow $ phương trình $(1)$ có $6$ nghiệm thuộc $(0,3\pi )\backslash \left\{ {\pi ,2\pi } \right\}.$
$ \Leftrightarrow $ phương trình $(2)$ có nghiệm thoả mãn $ – 1 < {t_1} < 0 < {t_2} < 1.$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{af( – 1) > 0}\\
{af(0) < 0}\\
{af(1) > 0}
\end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{3m + 2 > 0}\\
{m – 2 < 0}\\
{ – m + 2 > 0}
\end{array}} \right.$ $ \Leftrightarrow – \frac{2}{3} < m < 2.$
Vậy với $ – \frac{2}{3} < m < 2$ thoả mãn điều kiện đầu bài.

Chú ý: Để các em học sinh tiện theo dõi ta có thể lý giải điều kiện trên có được bởi:
1. Với ${t_2} \in (0,1)$ thì bằng cách dựng đường thẳng qua ${t_2}$ vuông góc với trục sin ta được bốn nghiệm ${\alpha _1}$, ${\alpha _2}$, ${\alpha _3}$ và ${\alpha _4}$ thuộc cung $\widehat {AB}.$
2. Với ${t_1} \in ( – 1,0)$ thì bằng cách dựng đường thẳng qua ${t_1}$ vuông góc với trục sin ta được hai nghiệm ${\alpha _5}$ và ${\alpha _6}$ thuộc cung $\widehat {AB}.$
III. BÀI TẬP ĐỀ NGHỊ
Bài tập 1: Giải phương trình: $4(\sin 3x – \cos 2x) = 5(\sin x – 1).$
Bài tập 2: Cho phương trình: $\sin 3x + \sin x – 2{\cos ^2}x = m.$
a. Giải phương trình với $m = 0.$
b. Tìm $m$ để phương trình có $6$ nghiệm phân biệt thuộc $[0,\pi ].$
Bài tập 3: Xác định $m$ để phương trình: ${\cos ^4}x + (m – 2){\sin ^2}x + 4 = 0$ vô nghiệm.









