Tài liệu gồm 206 trang, được biên soạn bởi nhóm Toán thầy Lê Văn Đoàn: Ths. Lê Văn Đoàn – Ths. Trương Huy Hoàng – Ths. Nguyễn Tiến Hà – Bùi Sỹ Khanh – Nguyễn Đức Nam – Đỗ Minh Tiến, phân dạng và tuyển chọn các bài toán thuộc chương trình Giải tích 12 giai đoạn học kì 1: ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số, hàm số luỹ thừa, hàm số mũ, hàm số logarit.
CHƯƠNG 1. ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ.
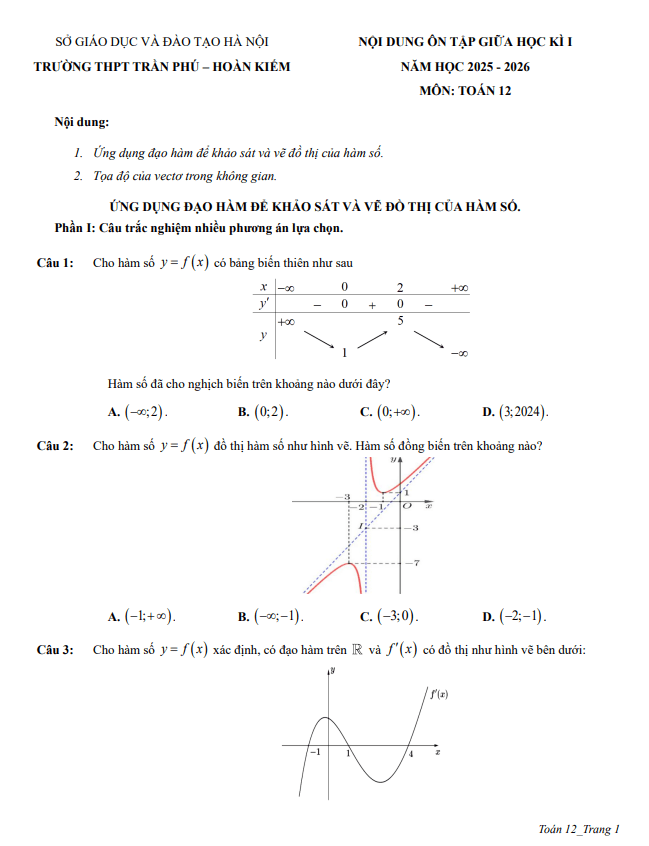
BÀI 1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ.
+ Dạng toán 1: Tìm các khoảng đơn điệu (khảo sát chiều biến thiên).
+ Dạng toán 2. Tìm tham số m để hàm số đơn điệu trên miền xác định của nó.
+ Dạng toán 3. Một số bài toán vận dụng và vận dụng cao thường gặp.
BÀI 2. CỰC TRỊ CỦA HÀM SỐ
+ Dạng toán 1: Tìm điểm cực đại, cực tiểu, giá trị cực đại, giá trị cực tiểu.
+ Dạng toán 2. Tìm tham số m để hàm số đạt cực trị tại điểm x = xo cho trước.
+ Dạng toán 3. Biện luận hoành độ cực trị hoặc tung độ cực trị.
+ Dạng toán 4. Một số bài toán vận dụng và vận dụng cao thường gặp.
BÀI 3. GIÁ TRỊ LỚN NHẤT VÀ GIÁ TRỊ NHỎ NHẤT CỦA HÀM SỐ.
+ Dạng toán 1: Tìm GTNN và GTLN của hàm số khi đề cho đồ thị hoặc bảng biến thiên.
+ Dạng toán 2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn.
+ Dạng toán 3. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên khoảng.
+ Dạng toán 4. Một số bài toán vận dụng và vận dụng cao thường gặp.
BÀI 4. ĐƯỜNG TIỆM CẬN.
+ Dạng toán 1: Tìm đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số.
+ Dạng toán 2. Bài toán tiệm cận liên quan đến tham số.
BÀI 5. KHẢO SÁT SỰ BIẾN THIÊN VÀ VẼ ĐỒ THỊ HÀM SỐ.
+ Dạng toán 1: Nhận dạng đồ thị hàm số.
+ Dạng toán 2. Biến đổi đồ thị.
+ Dạng toán 3. Tương giao khi đề cho bảng biến thiên hoặc đồ thị.
+ Dạng toán 4. Tương giao của hai hàm cụ thể.
[ads]
CHƯƠNG 2. HÀM SỐ LUỸ THỪA, HÀM SỐ MŨ, HÀM SỐ LOGARIT.
BÀI 1. CÔNG THỨC MŨ VÀ LOGARIT.
+ Dạng toán 1: Công thức mũ và các biến đổi.
+ Dạng toán 2. Công thức lôgarit và các biến đổi.
BÀI 2. HÀM SỐ LUỸ THỪA – HÀM SỐ MŨ – HÀM SỐ LOGARIT.
+ Dạng toán 1: Tìm tập xác định của hàm lũy thừa, mũ, lôgarit.
+ Dạng toán 2. Tìm đạo hàm của hàm mũ – lôgarit.
+ Dạng toán 3. Đơn điệu và cực trị của hàm số mũ và lôgarit.
+ Dạng toán 4. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số mũ và lôgarit.
+ Dạng toán 5. Nhận dạng đồ thị hàm số mũ – lũy thừa và lôgarit.
+ Dạng toán 5. Bài toán lãi suất và một số bài toán thực tế khác.
BÀI 3. PHƯƠNG TRÌNH MŨ, PHƯƠNG TRÌNH LOGARIT.
+ Dạng toán 1: Phương trình mũ và lôgarit cơ bản (hay đưa về cùng cơ số).
+ Dạng toán 2. Giải phương trình mũ – lôgarit bằng cách đặt ẩn phụ.
+ Dạng toán 3. Bài toán chứa tham số trong phương trình mũ và lôgarit (nâng cao).
+ Dạng toán 4. Phương pháp hàm số (nâng cao).
BÀI 4. BẤT PHƯƠNG TRÌNH MŨ – BẤT PHƯƠNG TRÌNH LOGARIT.
+ Dạng toán 1: Bất phương trình mũ và lôgarit cơ bản hoặc đưa về cùng cơ số.
+ Dạng toán 2. Phương pháp đặt ẩn phụ hoặc phương pháp đánh giá.
+ Dạng toán 3. Tìm m để bất phương trình nghiệm đúng, có nghiệm (nâng cao).