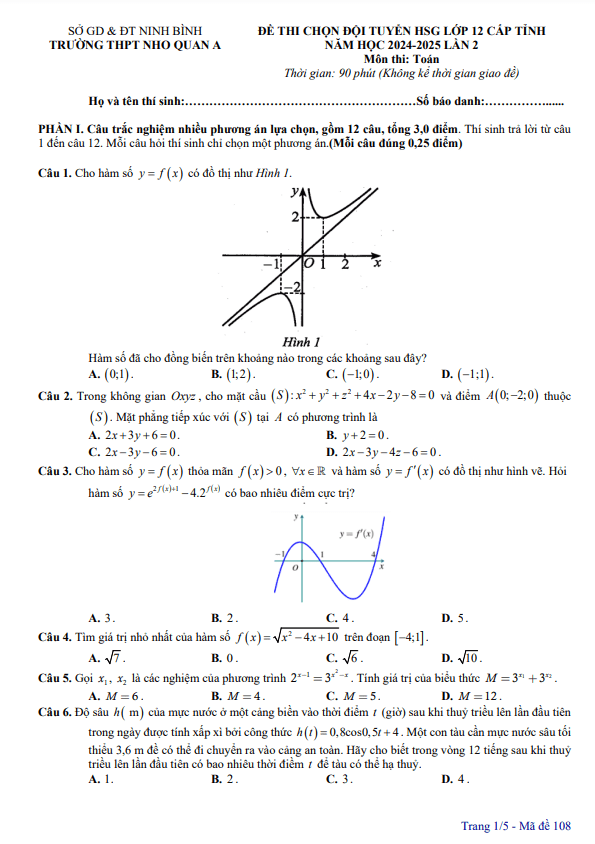
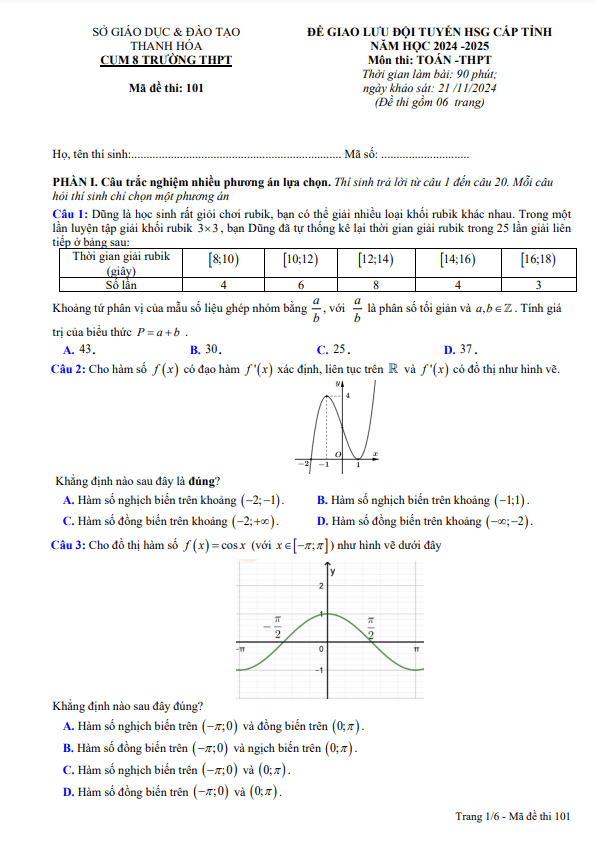
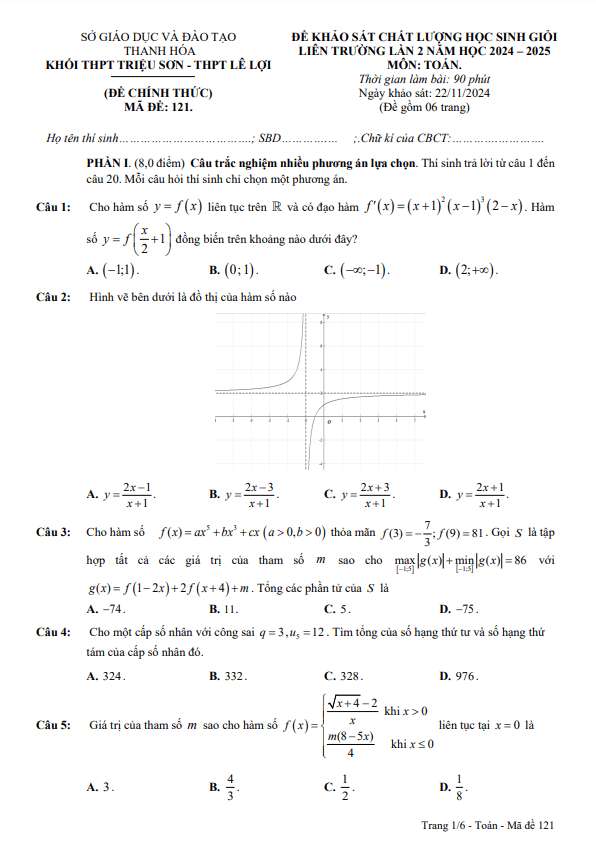TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi chọn đội tuyển dự thi học sinh giỏi cấp Quốc gia môn Toán THPT năm học 2024 – 2025 sở Giáo dục và Đào tạo tỉnh Bình Dương. Kỳ thi được diễn ra trong 02 ngày: ngày thi thứ nhất 19/09/2024 và ngày thi thứ hai 20/09/2024.
Trích dẫn Đề chọn đội tuyển thi HSG QG môn Toán THPT năm 2024 – 2025 sở GD&ĐT Bình Dương:
+ Cho tam giác ABC không cân, nội tiếp đường tròn (O). Hai đường cao BE, CF cắt nhau tại trực tâm H. Đường thẳng EF cắt BC tại K. Qua K kẻ đường thẳng vuông góc với BC cắt CH, BH lần lượt tại P, Q. Đường thẳng AH cắt (O) tại T khác A. Đường thẳng qua H vuông góc với EF cắt BC tại L. a) Chứng minh LT tiếp xúc với đường tròn (HPQ). b) Dựng đường kính AA’ của (O). Đường thẳng qua L vuông góc với BC cắt A’B, A’C lần lượt tại Y, Z. Chứng minh rằng đường tròn (A’YZ) tiếp xúc với đường tròn (HPQ).
+ Cho a1, a2, a3, a4, a5, a6 là 6 số tự nhiên không vượt quá 20. Gọi m là trung bình cộng của 6 số đã cho. Hai số được gọi là một “cặp số đẹp” nếu như trung bình cộng chúng lớn hơn m. a) Chứng minh rằng không thể chia 6 số đã cho thành 3 cặp đều là các “cặp số đẹp”. b) Trong 6 số đã cho, có thể có nhiều nhất bao nhiêu “cặp số đẹp”?
+ Tìm số tập con A của X = {1; 2; 3; …; 2023} sao cho tổng các phần tử của A chia hết cho 7.