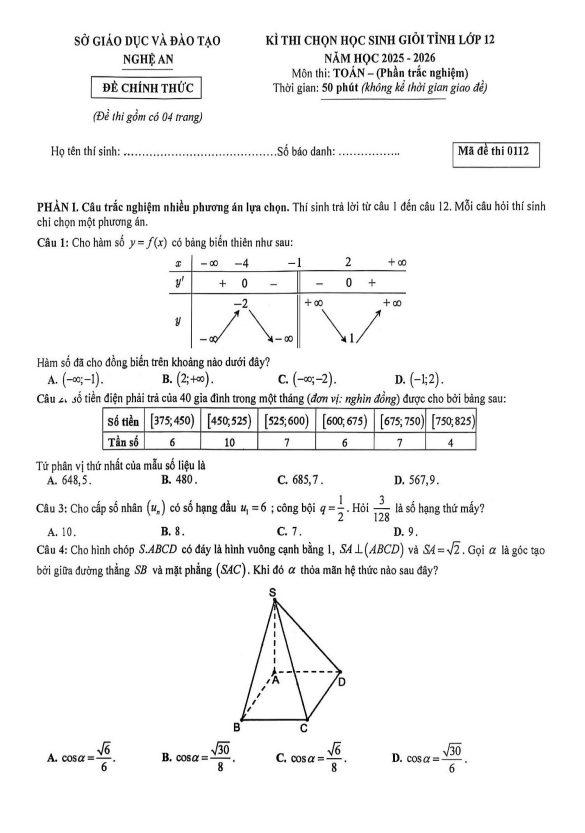
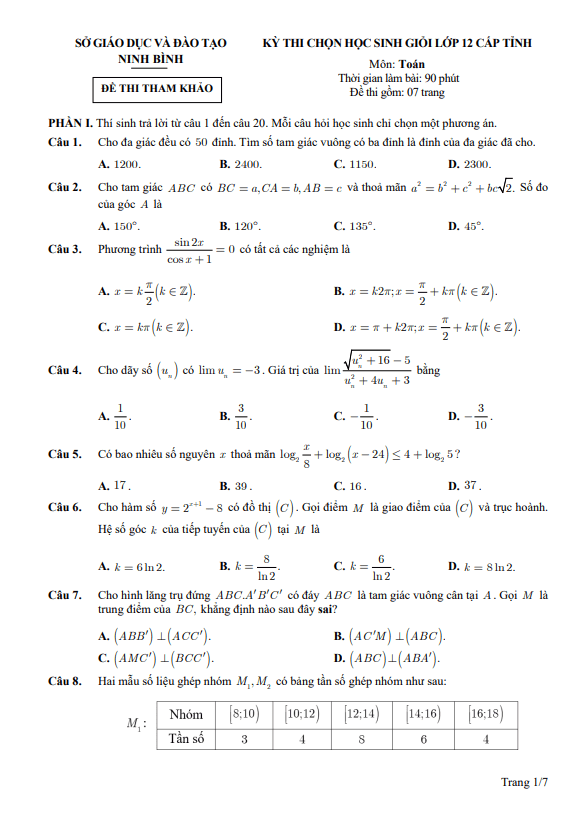TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh đề thi chọn đội tuyển học sinh giỏi môn Toán vòng 1 năm học 2025 – 2026 trường THPT Bỉm Sơn, tỉnh Thanh Hóa. Đề thi gồm 20 câu trắc nghiệm nhiều lựa chọn + 06 câu đúng sai + 06 câu trả lời ngắn, thời gian làm bài 90 phút, có đáp án và lời giải chi tiết.
Trích dẫn Đề chọn đội tuyển HSG Toán vòng 1 năm 2025 – 2026 trường THPT Bỉm Sơn – Thanh Hóa:
+ Trong trận thi đấu bóng bàn đơn nam giữa vận động viên Nguyễn Đức Tuân (người từng đoạt huy chương vàng đơn nam môn bóng bàn tại Seagames 31) với một vận động viên nước ngoài, trận đấu gồm tối đa 5 set (séc), người nào thắng trước 3 set sẽ giành chiến thắng chung cuộc. Xác suất để vận động viên Tuân thắng mỗi set là 0,6. Tính xác suất để vận động viên Tuân giành chiến thắng trong trận đấu (làm tròn kết quả đến hàng phần trăm).
+ Một bồn hoa hình tròn ở giữa sân trường được chia thành 6 phần bằng nhau và giao nhiệm vụ cho 6 lớp 10 chọn trồng một trong 4 loại hoa là hoa cúc, hoa hồng, hoa lan, hoa hướng dương theo các khu vực hình quạt được phân công cụ thể như hình vẽ. Tính xác suất để hai lớp được phân công hai khu vực cạnh nhau thì không cùng trồng một loại hoa? (làm tròn đến hàng phân trăm).
+ Giả sử số lượng tế bào của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hoá bằng hàm số P(t) = a/(b + e^-0,75t), trong đó thời gian t được tính bằng giờ. Tại thời điểm ban đầu t = 0, quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Theo mô hình này số lượng tế bào của quần thể luôn thuộc nửa khoảng [α;β). Khi đó α + β bằng bao nhiêu?
File WORD (dành cho quý thầy, cô): TẢI XUỐNG