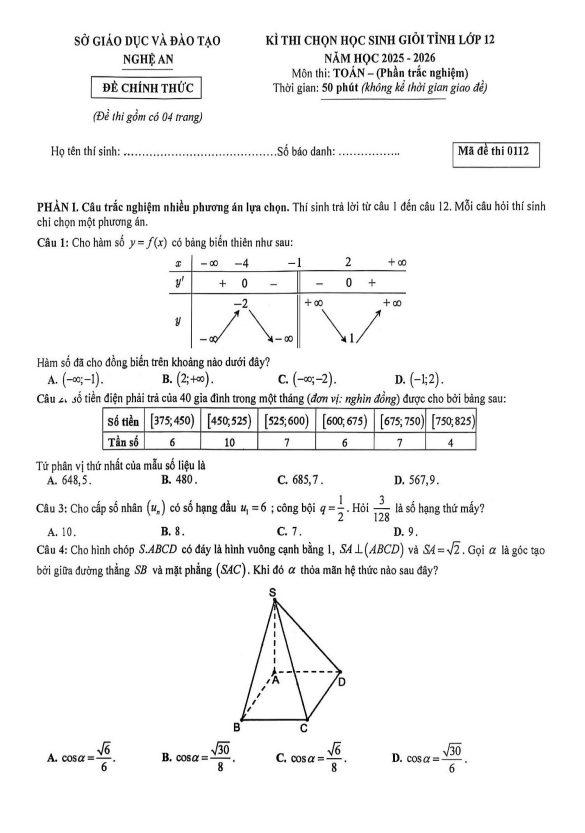
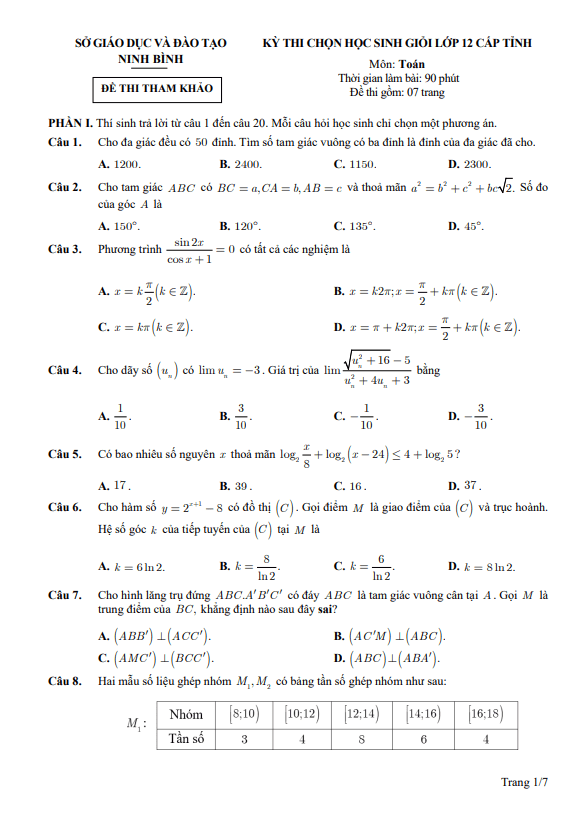TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh đề chính thức kỳ thi chọn đội tuyển dự thi học sinh giỏi Quốc gia môn Toán THPT năm học 2025 – 2026 sở Giáo dục và Đào tạo tỉnh Lào Cai. Kỳ thi được diễn ra vào ngày 16 và ngày 17 tháng 09 năm 2025.
Trích dẫn Đề chọn đội tuyển thi HSG QG môn Toán THPT năm 2025 – 2026 sở GD&ĐT Lào Cai:
+ Cho tam giác ABC nhọn, không cân (AB < AC) và nội tiếp đường tròn tâm O. Tam giác ABC có các đường cao AD, BE và CF cắt nhau tại H. Gọi M là trung điểm của cạnh BC. Đường tròn tâm J ngoại tiếp tam giác AEF cắt đường tròn (O) tại điểm thứ hai là K; đường thẳng AK cắt đường thẳng BC tại L; đường thẳng AM cắt đường tròn (J) tại điểm thứ hai là Q. 1) Chứng minh ba điểm L, H, Q thẳng hàng; các đường thẳng KF, EQ và BC đồng quy hoặc đôi một song song. 2) Gọi P là giao điểm của hai đường thẳng EF và AD; đoạn thẳng PM cắt đường tròn (J) tại điểm N. Chứng minh rằng đường thẳng LN là tiếp tuyến chung của đường tròn ngoại tiếp tam giác DMN và đường tròn ngoại tiếp tam giác BNC.
+ Cho tập A = {1; 2; 3; …; 2025} . Tìm số nguyên dương k lớn nhất (k > 2) sao cho ta có thể chọn được k số phân biệt từ tập A mà tổng của hai số phân biệt bất kỳ trong k số được chọn không chia hết cho hiệu của chúng.