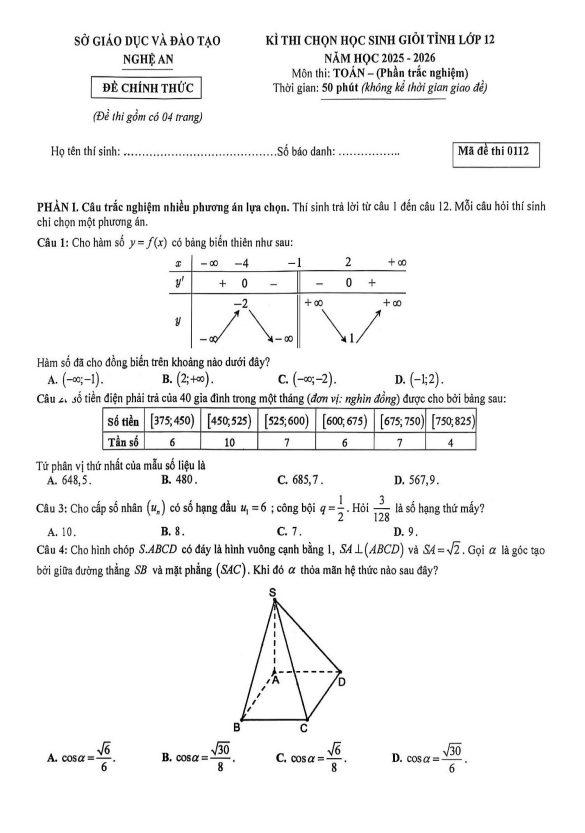
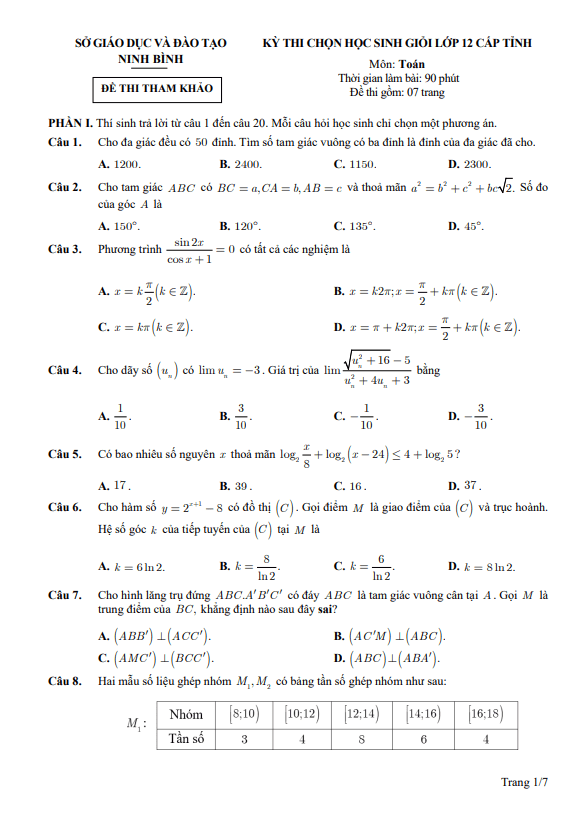TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh đề chính thức kỳ thi lập đội tuyển dự thi chọn học sinh giỏi Quốc gia môn Toán THPT năm học 2025 – 2026 sở Giáo dục và Đào tạo tỉnh Đắk Lắk. Kỳ thi được diễn ra vào ngày 17 và ngày 18 tháng 09 năm 2025.
Trích dẫn Đề lập đội tuyển thi HSG QG môn Toán THPT năm 2025 – 2026 sở GD&ĐT Đắk Lắk:
+ Cho các số nguyên a, b, c và số nguyên tố p thỏa mãn a/b + b/c + c/a = p. Chứng minh rằng abc là lũy thừa bậc 3 của một số nguyên.
+ Cho tam giác ABC nội tiếp đường tròn (O). Hai đường cao kẻ từ B, C cắt (O) lần lượt tại E, F và cắt nhau tại H. Gọi (C1) là đường tròn qua E, H và tiếp xúc CH tại H; (C2) là đường tròn qua F, H và tiếp xúc BH tại H. Gọi G là giao điểm của (C1) và (C2) khác điểm H. a) Chứng minh rằng: AG vuông góc GH. b) Chứng minh rằng: Điểm G nằm trên đường tròn (O).
+ Gọi X là tập hợp các số nguyên dương không vượt quá 2025. Xét tất cả các tập hợp A là tập con của X thỏa mãn: “Nếu x, y là hai phần tử bất kỳ của A thì |x – y| không thuộc {20;30}. Hỏi số phần tử nhiều nhất trong những tập hợp A đó là bao nhiêu?