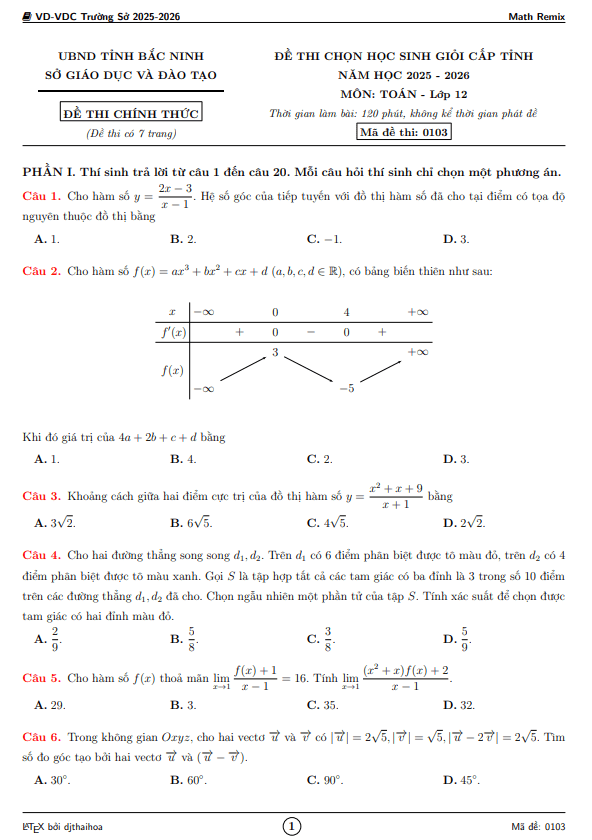
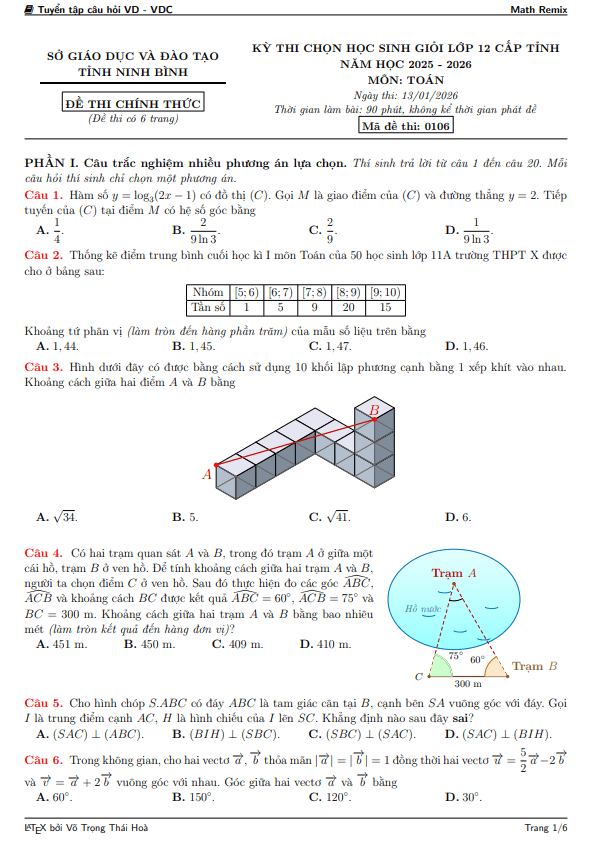
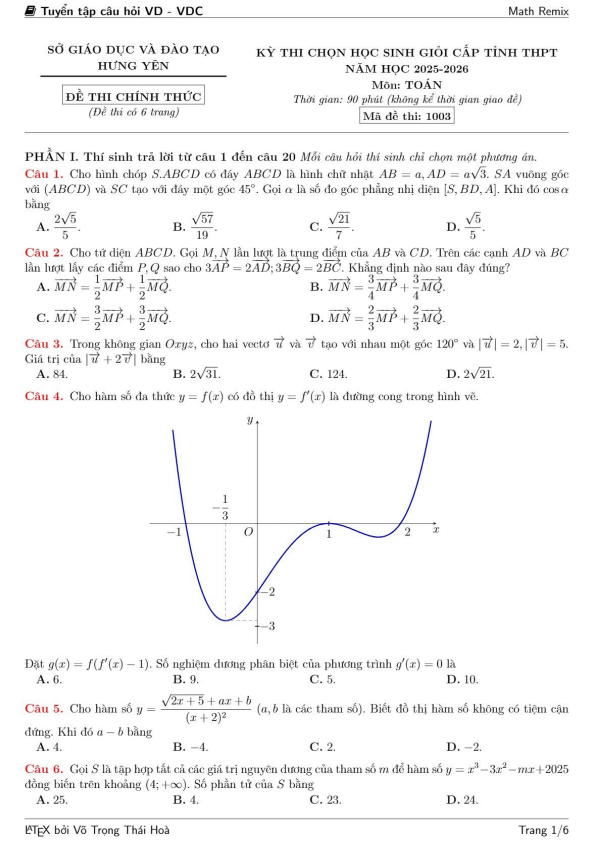
TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh đề thi chọn học sinh giỏi cấp tỉnh môn Toán THPT năm học 2025 – 2026 sở Giáo dục và Đào tạo tỉnh Đồng Nai (bảng A và bảng B). Kỳ thi được diễn ra vào ngày 22 tháng 01 năm 2026.
Trích dẫn Đề chọn học sinh giỏi tỉnh Toán THPT năm 2025 – 2026 sở GD&ĐT Đồng Nai:
+ Xét dãy vô hạn các hình vuông V1, V2, V3, … được đặt kề nhau như hình vẽ. Trong đó, V1 có cạnh bằng 1 và kể từ hình vuông thứ hai trở đi, mỗi hình vuông có cạnh bằng 3/4 cạnh hình vuông kề trước nó. Một con kiến xuất phát từ đỉnh A của V1, đi ngang sang phải và dọc xuống dưới theo các nét tô đậm của tất cả các hình vuông. Tính quãng đường đi được của con kiến.
+ An cần mua một số hộp bánh để dùng trong những ngày Tết, cụ thể như sau: – Hộp nhỏ: ít nhất 3 hộp và nhiều nhất 10 hộp với giá 100 nghìn đồng mỗi hộp. – Hộp lớn: ít nhất 1 hộp và nhiều nhất 5 hộp với giá 300 nghìn đồng mỗi hộp. Cửa hàng sẽ miễn phí giao hàng nếu giá đơn hàng tối thiểu 900 nghìn đồng. Hỏi An cần mua tối thiểu bao nhiêu hộp bánh (gồm cả hộp nhỏ và hộp lớn) để được miễn phí giao hàng?
+ Một hàng rào cao 2 mét, song song và cách bức tường của một ngôi nhà 1 mét. Đặt một cái thang sao cho đầu thang tựa vào tường, chân thang ở bên ngoài hàng rào và thân thang vừa chạm hàng rào như hình vẽ. Giả sử chiều dài thang là l mét và khoảng cách từ chân thang đến hàng rào là x mét. a) Tính l theo x. b) Tìm giá trị nhỏ nhất của l.