Bài viết trình bày công thức tính khoảng cách giữa hai đường thẳng chéo nhau trong hệ trục tọa độ không gian Oxyz và hướng dẫn áp dụng công thức giải một số bài tập trắc nghiệm liên quan.
1. PHƯƠNG PHÁP GIẢI TOÁN
Cho hai đường thẳng chéo nhau ${d_1}$ và ${d_2}$ có phương trình: ${d_1}:\left\{ {\begin{array}{*{20}{l}}
{x = {x_1} + {a_1}t}\\
{y = {y_1} + {b_1}t}\\
{z = {z_1} + {c_1}t}
\end{array}} \right.$ và ${d_2}:\left\{ {\begin{array}{*{20}{l}}
{x = {x_2} + {a_2}t’}\\
{y = {y_2} + {b_2}t’}\\
{z = {z_2} + {c_2}t’}
\end{array}} \right.$ $\left( {t;t’ \in R} \right).$ Ta tính khoảng cách giữa hai đường thẳng chéo nhau ${d_1}$ và ${d_2}$ theo một trong các cách sau:
Cách 1:
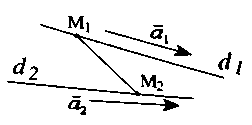
+ Bước 1: Xác định các vectơ chỉ phương ${\vec a_1}$ của ${d_1}$, ${\vec a_2}$ của ${d_2}.$
+ Bước 2: Xác định các điểm ${M_1} \in {d_1}$, ${M_2} \in {d_2}.$
+ Bước 3: Lúc đó $d\left( {{d_1};{d_2}} \right)$ $ = \frac{{\left| {\left[ {{{\vec a}_1},{{\vec a}_2}} \right].\overrightarrow {{M_1}{M_2}} } \right|}}{{\left| {\left[ {{{\vec a}_1},{{\vec a}_2}} \right]} \right|}}.$
Cách 2:
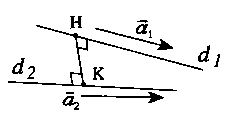
+ Bước 1: Gọi $H \in {d_1}$, $K \in {d_2}$ (lúc này $H$, $K$ có toạ độ phụ thuộc ẩn $t$, $t’$).
+ Bước 2: Xác định $H$, $K$ dựa vào:
$\left\{ {\begin{array}{*{20}{l}}
{HK \bot {d_1}}\\
{HK \bot {d_2}}
\end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {HK} .{{\vec a}_1} = 0}\\
{\overrightarrow {HK} .{{\vec a}_2} = 0}
\end{array}} \right..$
+ Bước 3: Lúc đó: $d\left( {{d_1};{d_2}} \right) = HK.$
Nhận xét: Trong nhiều bài toán yêu cầu viết phương trình đường vuông góc chung thì nên sử dụng cách 2.
2. BÀI TẬP ÁP DỤNG
Ví dụ 1: Trong không gian với hệ tọa độ $Oxyz$, tính khoảng cách $d$ từ giữa hai đường thẳng ${\Delta _1}:\frac{{x – 2}}{{ – 1}} = \frac{{y – 1}}{2} = \frac{{z – 2}}{{ – 1}}$, ${\Delta _2}:\frac{{x – 1}}{2} = \frac{y}{{ – 1}} = \frac{{z – 1}}{{ – 1}}.$
A. $d = \sqrt 3 .$
B. $d = \frac{{3\sqrt 3 }}{2}.$
C. $d = 2\sqrt 3 .$
D. $d = 3\sqrt 3 .$
Lời giải:
Kiểm tra được ${\Delta _1}$ và ${\Delta _2}$ chéo nhau.
Cách 1: (Tính độ dài đoạn vuông góc chung).
Đường thẳng ${\Delta _1}$ có một vectơ chỉ phương là ${\vec u_1} = ( – 1;2; – 1).$
Đường thẳng ${\Delta _2}$ có một vectơ chỉ phương là ${\vec u_2} = (2; – 1; – 1).$
Ta có ${\Delta _1}:\left\{ {\begin{array}{*{20}{l}}
{x = 2 – t}\\
{y = 1 + 2t}\\
{z = 2 – t}
\end{array}} \right.$ và ${\Delta _2}:\left\{ {\begin{array}{*{20}{l}}
{x = 1 + 2k}\\
{y = – k}\\
{z = 1 – k}
\end{array}} \right..$
Gọi $H(2 – t;1 + 2t;2 – t) \in {\Delta _1}$, $K(1 + 2k; – k;1 – k) \in {\Delta _2}.$
$HK$ là đoạn vuông góc chung của ${\Delta _1}$ và ${\Delta _2}$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {HK} .{{\vec u}_1} = 0}\\
{\overrightarrow {HK} .{{\vec u}_2} = 0}
\end{array}} \right..$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{t = 0}\\
{k = 0}
\end{array}} \right.$ $ \Rightarrow H(2;1;2)$, $K(1;0;1)$ $ \Rightarrow \overrightarrow {HK} = ( – 1; – 1; – 1)$ $ \Rightarrow d\left( {{\Delta _1};{\Delta _2}} \right) = HK = \sqrt 3 .$
Cách 2: (Sử dụng công thức).
Đường thẳng ${\Delta _1}$ có một vectơ chỉ phương là ${\vec u_1} = ( – 1;2; – 1).$
Đường thẳng ${\Delta _2}$ có một vectơ chỉ phương là ${\vec u_2} = (2; – 1; – 1).$
Chọn $A(2;1;2) \in {\Delta _1}$, $B(1;0;1) \in {\Delta _2}$ $ \Rightarrow \overrightarrow {AB} = ( – 1; – 1; – 1).$
Lúc đó: $d = \frac{{\left| {\overrightarrow {AB} .\left[ {{{\vec u}_1},{{\vec u}_2}} \right]} \right|}}{{\left| {\left[ {{{\vec u}_1},{{\vec u}_2}} \right]} \right|}} = \sqrt 3 .$
Chọn đáp án A.
Ví dụ 2: Trong không gian với hệ tọa độ $Oxyz$, gọi $M$, $N$ là các điểm bất kì lần lượt thuộc ${\Delta _1}:\frac{{x – 2}}{{ – 1}} = \frac{{y – 1}}{2} = \frac{{z – 2}}{{ – 1}}$ và ${\Delta _2}:\frac{{x – 1}}{2} = \frac{y}{{ – 1}} = \frac{{z – 1}}{{ – 1}}.$ Tính độ dài ngắn nhất của đoạn thẳng $MN.$
A. $2\sqrt 3 .$
B. $\sqrt 3 .$
C. $4\sqrt 3 .$
D. $\frac{{3\sqrt 3 }}{2}.$
Lời giải:
Kiểm tra được ${\Delta _1}$ và ${\Delta _2}$ chéo nhau. Độ dài ngắn nhất của đoạn thẳng $MN$ là khoảng cách giữa hai đường thẳng ${\Delta _1}$ và ${\Delta _2}.$
Đường thẳng ${\Delta _1}$ có một vectơ chỉ phương là ${\vec u_1} = ( – 1;2; – 1).$
Đường thẳng ${\Delta _2}$ có một vectơ chỉ phương là ${\vec u_2} = (2; – 1; – 1).$
Chọn $A(2;1;2) \in {\Delta _1}$, $B(1;0;1) \in {\Delta _2}$ $ \Rightarrow \overrightarrow {AB} = ( – 1; – 1; – 1).$
Lúc đó: $d = \frac{{\left| {\overrightarrow {AB} .\left[ {{{\vec u}_1},{{\vec u}_2}} \right]} \right|}}{{\left| {\left[ {{{\vec u}_1},{{\vec u}_2}} \right]} \right|}} = \sqrt 3 $ $ \Rightarrow M{N_{\min }} = \sqrt 3 .$
Chọn đáp án B.
Ví dụ 3: Trong không gian với hệ tọa độ $Oxyz$, viết phương trình mặt cầu có bán kính nhỏ nhất và đồng thời tiếp xúc với hai đường thẳng ${\Delta _1}:\frac{{x – 2}}{{ – 1}} = \frac{{y – 1}}{2} = \frac{{z – 2}}{{ – 1}}$, ${\Delta _2}:\frac{{x – 1}}{2} = \frac{y}{{ – 1}} = \frac{{z – 1}}{{ – 1}}.$
A. ${\left( {x – \frac{3}{2}} \right)^2} + {\left( {y – \frac{1}{2}} \right)^2} + {\left( {z – \frac{3}{2}} \right)^2} = 3.$
B. ${\left( {x + \frac{3}{2}} \right)^2} + {\left( {y + \frac{1}{2}} \right)^2} + {\left( {z + \frac{3}{2}} \right)^2} = \frac{3}{4}.$
C. ${\left( {x – \frac{3}{2}} \right)^2} + {\left( {y – \frac{1}{2}} \right)^2} + {\left( {z – \frac{3}{2}} \right)^2} = \frac{3}{4}.$
D. ${(x – 1)^2} + {(y – 2)^2} + {(z + 1)^2} = \frac{3}{4}.$
Lời giải:
Kiểm tra được ${\Delta _1}$ và ${\Delta _2}$ chéo nhau. Gọi $HK$ là đoạn vuông góc chung của ${\Delta _1}$ và ${\Delta _2}$ $ \Rightarrow $ mặt cầu cần tìm là mặt cầu có đường kính $HK.$
Đường thẳng ${\Delta _1}$ có một vectơ chỉ phương là ${\vec u_1} = ( – 1;2; – 1).$
Đường thẳng ${\Delta _2}$ có một vectơ chỉ phương là ${\vec u_2} = (2; – 1; – 1).$
Ta có ${\Delta _1}:\left\{ {\begin{array}{*{20}{l}}
{x = 2 – t}\\
{y = 1 + 2t}\\
{z = 2 – t}
\end{array}} \right.$ và ${\Delta _2}:\left\{ {\begin{array}{*{20}{l}}
{x = 1 + 2k}\\
{y = – k}\\
{z = 1 – k}
\end{array}} \right..$
Gọi $H(2 – t;1 + 2t;2 – t) \in {\Delta _1}$, $K(1 + 2k; – k;1 – k) \in {\Delta _2}.$
$HK$ là đoạn vuông góc chung của ${\Delta _1}$ và ${\Delta _2}$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {HK} .{{\vec u}_1} = 0}\\
{\overrightarrow {HK} .{{\vec u}_2} = 0}
\end{array}} \right..$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{t = 0}\\
{k = 0}
\end{array}} \right.$ $ \Rightarrow H(2;1;2)$, $K(1;0;1)$ $ \Rightarrow \overrightarrow {HK} = ( – 1; – 1; – 1)$ $ \Rightarrow HK = \sqrt 3 .$
Mặt cầu cần tìm có tâm $I\left( {\frac{3}{2};\frac{1}{2};\frac{3}{2}} \right)$ là trung điểm $HK$, bán kính $R = \frac{{HK}}{2} = \frac{{\sqrt 3 }}{2}$ có phương trình: $(S):{\left( {x – \frac{3}{2}} \right)^2} + {\left( {y – \frac{1}{2}} \right)^2} + {\left( {z – \frac{3}{2}} \right)^2} = \frac{3}{4}.$
Chọn đáp án C.
Ví dụ 4: Trong không gian với hệ tọa độ $Oxyz$, gọi $\vec u(1;a;b)$ $(a;b \in R)$ là một vectơ chỉ phương của đường vuông góc chung của hai đường thẳng ${\Delta _1}:\frac{{x – 2}}{{ – 1}} = \frac{{y – 1}}{2} = \frac{{z – 2}}{{ – 1}}$ và ${\Delta _2}:\frac{{x – 1}}{2} = \frac{y}{{ – 1}} = \frac{{z – 1}}{{ – 1}}.$ Tính tổng $S = a + b.$
A. $S=2.$
B. $S=-2.$
C. $S=4.$
D. $S=-4.$
Lời giải:
Kiểm tra được ${\Delta _1}$ và ${\Delta _2}$ chéo nhau.
Cách 1: (Tìm đoạn vuông góc chung).
Đường thẳng ${\Delta _1}$ có một vectơ chỉ phương là ${\vec u_1} = ( – 1;2; – 1).$
Đường thẳng ${\Delta _2}$ có một vectơ chỉ phương là ${\vec u_2} = (2; – 1; – 1).$
Ta có ${\Delta _1}:\left\{ {\begin{array}{*{20}{l}}
{x = 2 – t}\\
{y = 1 + 2t}\\
{z = 2 – t}
\end{array}} \right.$ và ${\Delta _2}:\left\{ {\begin{array}{*{20}{l}}
{x = 1 + 2k}\\
{y = – k}\\
{z = 1 – k}
\end{array}} \right..$
Gọi $H(2 – t;1 + 2t;2 – t) \in {\Delta _1}$, $K(1 + 2k; – k;1 – k) \in {\Delta _2}.$
$HK$ là đoạn vuông góc chung của ${\Delta _1}$ và ${\Delta _2}$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {HK} .{{\vec u}_1} = 0}\\
{\overrightarrow {HK} .{{\vec u}_2} = 0}
\end{array}} \right..$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{t = 0}\\
{k = 0}
\end{array}} \right.$ $ \Rightarrow H(2;1;2)$, $K(1;0;1)$ $ \Rightarrow \overrightarrow {HK} = ( – 1; – 1; – 1).$
Đường vuông góc chung có vectơ chỉ phương dạng $m\overrightarrow {HK} $ $(m \in R,m \ne 0)$, từ giả thiết suy ra $a = 1$, $b = 1$ $ \Rightarrow S = a + b = 2.$
Cách 2:
Đường thẳng ${\Delta _1}$ có một vectơ chỉ phương là ${\vec u_1} = ( – 1;2; – 1).$
Đường thẳng ${\Delta _2}$ có một vectơ chỉ phương là ${\vec u_2} = (2; – 1; – 1).$
Do $\vec u(1;a;b)$ là một vectơ chỉ phương của đường vuông góc chung của hai đường thẳng ${\Delta _1}$ và ${\Delta _2}$ suy ra:
$\left\{ {\begin{array}{*{20}{l}}
{\vec u.{{\vec u}_1} = 0}\\
{\vec u.{{\vec u}_2} = 0}
\end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{ – 1 + 2a – b = 0}\\
{2 – a – b = 0}
\end{array}} \right.$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{a = 1}\\
{b = 1}
\end{array}} \right.$ $ \Rightarrow \vec u = (1;1;1).$
Vậy $a = 1$, $b = 1$ $ \Rightarrow S = a + b = 2.$
Chọn đáp án A.
Ví dụ 5: Trong không gian với hệ tọa độ $Oxyz$, viết phương trình đường vuông góc chung của hai đường thẳng ${\Delta _1}:\frac{{x – 1}}{{ – 1}} = \frac{y}{1} = \frac{{z – 1}}{{ – 1}}$, ${\Delta _2}:\frac{{x – 2}}{4} = \frac{{y + 1}}{2} = \frac{{z + 1}}{1}.$
A. $\frac{{x – 1}}{1} = \frac{y}{1} = \frac{{z – 1}}{{ – 2}}.$
B. $\frac{{x – 1}}{1} = \frac{y}{2} = \frac{{z – 1}}{1}.$
C. $\frac{{x – 1}}{1} = \frac{y}{{ – 1}} = \frac{{z + 1}}{{ – 2}}.$
D. $\frac{{x – 1}}{1} = \frac{y}{{ – 1}} = \frac{{z – 1}}{{ – 2}}.$
Lời giải:
Kiểm tra được ${\Delta _1}$ và ${\Delta _2}$ chéo nhau.
Đường thẳng ${\Delta _1}$ có một vectơ chỉ phương là ${\vec u_1} = ( – 1;1; – 1).$
Đường thẳng ${\Delta _2}$ có một vectơ chỉ phương là ${\vec u_2} = (4;2;1).$
Ta có ${\Delta _1}:\left\{ {\begin{array}{*{20}{l}}
{x = 1 – t}\\
{y = t}\\
{z = 1 – t}
\end{array}} \right.$ và ${\Delta _2}:\left\{ {\begin{array}{*{20}{l}}
{x = 2 + 4k}\\
{y = – 1 + 2k}\\
{z = – 1 + k}
\end{array}} \right..$
Gọi $H(1 – t;t;1 – t) \in {\Delta _1}$, $K(2 + 4k; – 1 + 2k; – 1 + k) \in {\Delta _2}.$
$HK$ là đoạn vuông góc chung của ${\Delta _1}$ và ${\Delta _2}$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {HK} .{{\vec u}_1} = 0}\\
{\overrightarrow {HK} .{{\vec u}_2} = 0}
\end{array}} \right..$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{t = 0}\\
{k = 0}
\end{array}} \right.$ $ \Rightarrow H(1;0;1)$, $K(2; – 1; – 1)$ $ \Rightarrow \overrightarrow {HK} = (1; – 1; – 2).$
Đường vuông góc chung cần tìm là đường thẳng qua $H(1;0;1)$ và có một vectơ chỉ phương là $\overrightarrow {HK} = (1; – 1; – 2)$, có phương trình: $\frac{{x – 1}}{1} = \frac{y}{{ – 1}} = \frac{{z – 1}}{{ – 2}}.$
Chọn đáp án D.
Ví dụ 6: Trong không gian với hệ tọa độ $Oxyz$, tính khoảng cách $d$ từ giữa hai đường thẳng ${\Delta _1}:\left\{ {\begin{array}{*{20}{l}}
{x = 2 – 2t}\\
{y = 1 + t}\\
{z = 1}
\end{array}} \right.$, ${\Delta _2}:\frac{{x – 3}}{4} = \frac{{y – 3}}{{ – 1}} = \frac{{z – 3}}{{ – 1}}.$
A. $d = \sqrt 6 .$
B. $d = \frac{{3\sqrt 3 }}{2}.$
C. $d = 2\sqrt 3 .$
D. $d = 3.$
Lời giải:
Kiểm tra được ${\Delta _1}$ và ${\Delta _2}$ chéo nhau.
Cách 1: (Tính độ dài đoạn vuông góc chung).
Đường thẳng ${\Delta _1}$ có một vectơ chỉ phương là ${\vec u_1} = ( – 2;1;0).$
Đường thẳng ${\Delta _2}$ có một vectơ chỉ phương là ${\vec u_2} = (4; – 1; – 1).$
Ta có ${\Delta _1}:\left\{ {\begin{array}{*{20}{l}}
{x = 2 – 2t}\\
{y = 1 + t}\\
{z = 1}
\end{array}} \right.$ và ${\Delta _2}:\left\{ {\begin{array}{*{20}{l}}
{x = 3 + 4k}\\
{y = 3 – k}\\
{z = 3 – k}
\end{array}} \right..$
Gọi $H(2 – 2t;1 + t;1) \in {\Delta _1}$, $K(3 + 4k;3 – k;3 – k) \in {\Delta _2}.$
$HK$ là đoạn vuông góc chung của ${\Delta _1}$ và ${\Delta _2}$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {HK} .{{\vec u}_1} = 0}\\
{\overrightarrow {HK} .{{\vec u}_2} = 0}
\end{array}} \right..$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{t = 0}\\
{k = 0}
\end{array}} \right.$ $ \Rightarrow H(2;1;1)$, $K(3;3;3)$ $ \Rightarrow \overrightarrow {HK} = (1;2;2)$ $ \Rightarrow d\left( {{\Delta _1};{\Delta _2}} \right) = HK = 3.$
Cách 2: (Sử dụng công thức).
Đường thẳng ${\Delta _1}$ có một vectơ chỉ phương là ${\vec u_1} = ( – 2;1;0).$
Đường thẳng ${\Delta _2}$ có một vectơ chỉ phương là ${\vec u_2} = (4; – 1; – 1).$
Chọn $A(2;1;1) \in {\Delta _1}$, $B(3;3;3) \in {\Delta _2}$ $ \Rightarrow \overrightarrow {AB} = (1;2;2).$
Lúc đó: $d = \frac{{\left| {\overrightarrow {AB} .\left[ {{{\vec u}_1},{{\vec u}_2}} \right]} \right|}}{{\left| {\left[ {{{\vec u}_1},{{\vec u}_2}} \right]} \right|}} = 3.$
Chọn đáp án D.
Ví dụ 7: Trong không gian với hệ tọa độ $Oxyz$, viết phương trình đường vuông góc chung của hai đường thẳng: ${\Delta _1}:\left\{ {\begin{array}{*{20}{l}}
{x = 2 – 2t}\\
{y = 1 + t}\\
{z = 1}
\end{array}} \right.$, ${\Delta _2}:\frac{{x – 3}}{4} = \frac{{y – 3}}{{ – 1}} = \frac{{z – 3}}{{ – 1}}.$
A. $\frac{{x – 2}}{1} = \frac{{y – 1}}{2} = \frac{{z – 1}}{{ – 2}}.$
B. $\frac{{x – 2}}{1} = \frac{{y – 1}}{2} = \frac{{z – 1}}{2}.$
C. $\frac{{x – 2}}{1} = \frac{{y – 1}}{2} = \frac{{z + 1}}{2}.$
D. $\frac{{x – 1}}{1} = \frac{{y – 2}}{2} = \frac{{z – 2}}{2}.$
Lời giải:
Kiểm tra được ${\Delta _1}$ và ${\Delta _2}$ chéo nhau.
Đường thẳng ${\Delta _1}$ có một vectơ chỉ phương là ${\vec u_1} = ( – 2;1;0).$
Đường thẳng ${\Delta _2}$ có một vectơ chỉ phương là ${\vec u_2} = (4; – 1; – 1).$
Ta có ${\Delta _1}:\left\{ {\begin{array}{*{20}{l}}
{x = 2 – 2t}\\
{y = 1 + t}\\
{z = 1}
\end{array}} \right.$ và ${\Delta _2}:\left\{ {\begin{array}{*{20}{l}}
{x = 3 + 4k}\\
{y = 3 – k}\\
{z = 3 – k}
\end{array}} \right..$
Gọi $H(2 – 2t;1 + t;1) \in {\Delta _1}$, $K(3 + 4k;3 – k;3 – k) \in {\Delta _2}.$
$HK$ là đoạn vuông góc chung của ${\Delta _1}$ và ${\Delta _2}$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {HK} .{{\vec u}_1} = 0}\\
{\overrightarrow {HK} .{{\vec u}_2} = 0}
\end{array}} \right..$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{t = 0}\\
{k = 0}
\end{array}} \right.$ $ \Rightarrow H(2;1;1)$, $K(3;3;3)$ $ \Rightarrow \overrightarrow {HK} = (1;2;2).$
Đường vuông góc chung cần tìm là đường thẳng qua $H(2;1;1)$ và có một vectơ chỉ phương là $\overrightarrow {HK} = (1;2;2)$, có phương trình: $\frac{{x – 2}}{1} = \frac{{y – 1}}{2} = \frac{{z – 1}}{2}.$
Chọn đáp án B.
Ví dụ 8: Trong không gian với hệ tọa độ $Oxyz$, gọi $M$, $N$ là các điểm bất kì lần lượt thuộc ${\Delta _1}:\left\{ {\begin{array}{*{20}{l}}
{x = 2 – 2t}\\
{y = 1 + t}\\
{z = 1}
\end{array}} \right.$ và ${\Delta _2}:\frac{{x – 3}}{4} = \frac{{y – 3}}{{ – 1}} = \frac{{z – 3}}{{ – 1}}.$ Tính độ dài ngắn nhất của đoạn thẳng $MN.$
A. $2\sqrt 3 .$
B. $3.$
C. $4\sqrt 3 .$
D. $\frac{{3\sqrt 3 }}{2}.$
Lời giải:
Kiểm tra được ${\Delta _1}$ và ${\Delta _2}$ chéo nhau. Độ dài ngắn nhất của đoạn thẳng $MN$ là khoảng cách giữa hai đường thẳng ${\Delta _1}$ và ${\Delta _2}.$
Đường thẳng ${\Delta _1}$ có một vectơ chỉ phương là ${\vec u_1} = ( – 2;1;0).$
Đường thẳng ${\Delta _2}$ có một vectơ chỉ phương là ${\vec u_2} = (4; – 1; – 1).$
Chọn $A(2;1;1) \in {\Delta _1}$, $B(3;3;3) \in {\Delta _2}$ $ \Rightarrow \overrightarrow {AB} = (1;2;2).$
Lúc đó: $d = \frac{{\left| {\overrightarrow {AB} .\left[ {{{\vec u}_1},{{\vec u}_2}} \right]} \right|}}{{\left| {\left[ {{{\vec u}_1},{{\vec u}_2}} \right]} \right|}} = 3$ $ \Rightarrow M{N_{\min }} = 3.$
Chọn đáp án B.
Ví dụ 9: Trong không gian với hệ tọa độ $Oxyz$, viết phương trình mặt cầu có bán kính nhỏ nhất và đồng thời tiếp xúc với hai đường thẳng ${\Delta _1}:\left\{ {\begin{array}{*{20}{l}}
{x = 2 – 2t}\\
{y = 1 + t}\\
{z = 1}
\end{array}} \right.$, ${\Delta _2}:\frac{{x – 3}}{4} = \frac{{y – 3}}{{ – 1}} = \frac{{z – 3}}{{ – 1}}.$
A. ${\left( {x – \frac{5}{2}} \right)^2} + {(y – 2)^2} + {(z + 2)^2} = \frac{9}{4}.$
B. ${\left( {x – \frac{5}{2}} \right)^2} + {(y – 2)^2} + {(z – 2)^2} = \frac{9}{4}.$
C. ${\left( {x – \frac{5}{2}} \right)^2} + {(y – 2)^2} + {(z – 2)^2} = \frac{9}{2}.$
D. ${\left( {x + \frac{5}{2}} \right)^2} + {(y + 2)^2} + {(z + 2)^2} = \frac{9}{4}.$
Lời giải:
Kiểm tra được ${\Delta _1}$ và ${\Delta _2}$ chéo nhau. Gọi $HK$ là đoạn vuông góc chung của ${\Delta _1}$ và ${\Delta _2}$, suy ra mặt cầu cần tìm là mặt cầu có đường kính $HK.$
Đường thẳng ${\Delta _1}$ có một vectơ chỉ phương là ${\vec u_1} = ( – 2;1;0).$
Đường thẳng ${\Delta _2}$ có một vectơ chỉ phương là ${\vec u_2} = (4; – 1; – 1).$
Ta có ${\Delta _1}:\left\{ {\begin{array}{*{20}{l}}
{x = 2 – 2t}\\
{y = 1 + t}\\
{z = 1}
\end{array}} \right.$ và ${\Delta _2}:\left\{ {\begin{array}{*{20}{l}}
{x = 3 + 4k}\\
{y = 3 – k}\\
{z = 3 – k}
\end{array}} \right..$
Gọi $H(2 – 2t;1 + t;1) \in {\Delta _1}$, $K(3 + 4k;3 – k;3 – k) \in {\Delta _2}.$
$HK$ là đoạn vuông góc chung của ${\Delta _1}$ và ${\Delta _2}$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\overrightarrow {HK} .{{\vec u}_1} = 0}\\
{\overrightarrow {HK} .{{\vec u}_2} = 0}
\end{array}} \right..$
$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{t = 0}\\
{k = 0}
\end{array}} \right.$ $ \Rightarrow H(2;1;1)$, $K(3;3;3)$ $ \Rightarrow \overrightarrow {HK} = (1;2;2)$ $ \Rightarrow HK = 3.$
Mặt cầu cần tìm có tâm $I\left( {\frac{5}{2};2;2} \right)$ là trung điểm $HK$, bán kính $R = \frac{{HK}}{2} = \frac{3}{2}$ có phương trình: $(S):{\left( {x – \frac{5}{2}} \right)^2} + {(y – 2)^2} + {(z – 2)^2} = \frac{9}{4}.$
Chọn đáp án B.
Ví dụ 10: Trong không gian với hệ tọa độ $Oxyz$, tính khoảng cách $d$ từ giữa hai đường thẳng $\Delta :\frac{{x – 1}}{2} = \frac{y}{1} = \frac{{z + 4}}{1}$ và trục $Oy.$
A. $d = \frac{{3\sqrt 5 }}{5}.$
B. $d = \frac{{3\sqrt 3 }}{2}.$
C. $d = \frac{{7\sqrt 5 }}{5}.$
D. $d = 3.$
Lời giải:
Kiểm tra được $\Delta $ và $Oy$ chéo nhau.
Đường thẳng $\Delta $ có một vectơ chỉ phương là ${\vec u_\Delta } = (2;1; – 1).$
Đường thẳng chứa trục $Oy$ có một vectơ chỉ phương là $\vec u = (0;1;0).$
Chọn $O(0;0;0) \in Oy$, $A(1;0; – 4) \in \Delta $ $ \Rightarrow \overrightarrow {OA} = (1;0; – 4).$
Lúc đó: $d = \frac{{\left| {\overrightarrow {OA} .\left[ {\vec u,{{\vec u}_\Delta }} \right]} \right|}}{{\left| {\left[ {\vec u,{{\vec u}_\Delta }} \right]} \right|}} = \frac{{7\sqrt 5 }}{5}.$
Chọn đáp án C.
3. BÀI TẬP TỰ LUYỆN
1. ĐỀ BÀI
Câu 1: Trong không gian với hệ tọa độ $Oxyz$, viết phương trình đường vuông góc chung của hai đường thẳng ${\Delta _1}:\frac{{x – 2}}{{ – 1}} = \frac{{y – 1}}{2} = \frac{{z – 2}}{{ – 1}}$, $\Delta_{2}: \frac{x-1}{2}=\frac{y}{-1}=\frac{z-1}{-1}.$
A. $\frac{{x – 1}}{1} = \frac{{y – 1}}{2} = \frac{{z – 1}}{1}.$
B. $\frac{{x – 1}}{1} = \frac{y}{2} = \frac{{z – 1}}{1}.$
C. $\frac{{x + 1}}{1} = \frac{y}{1} = \frac{{z + 1}}{1}.$
D. $\frac{{x – 1}}{1} = \frac{y}{1} = \frac{{z – 1}}{1}.$
Câu 2: Trong không gian với hệ tọa độ $Oxyz$, tính khoảng cách $d$ từ giữa hai đường thẳng ${\Delta _1}:\frac{{x – 1}}{{ – 1}} = \frac{y}{1} = \frac{{z – 1}}{{ – 1}}$, ${\Delta _2}:\frac{{x – 2}}{4} = \frac{{y + 1}}{2} = \frac{{z + 1}}{1}.$
A. $d = \sqrt 6 .$
B. $d = \frac{{3\sqrt 3 }}{2}.$
C. $d = 2\sqrt 3 .$
D. $d = 3\sqrt 3 .$
Câu 3: Trong không gian với hệ tọa độ $Oxyz$, gọi $M$, $N$ là các điểm bất kì lần lượt thuộc ${\Delta _1}:\frac{{x – 1}}{{ – 1}} = \frac{y}{1} = \frac{{z – 1}}{{ – 1}}$ và ${\Delta _2}:\frac{{x – 2}}{4} = \frac{{y + 1}}{2} = \frac{{z + 1}}{1}.$ Tính độ dài ngắn nhất của đoạn thẳng $MN.$
A. $2\sqrt 3 .$
B. $\sqrt 6 .$
C. ${4\sqrt 3 .}$
D. ${\frac{{3\sqrt 3 }}{2}.}$
Câu 4: Trong không gian với hệ tọa độ $Oxyz$, viết phương trình mặt cầu có bán kính nhỏ nhất và đồng thời tiếp xúc với hai đường thẳng ${\Delta _1}:\frac{{x – 1}}{{ – 1}} = \frac{y}{1} = \frac{{z – 1}}{{ – 1}}$, ${\Delta _2}:\frac{{x – 2}}{4} = \frac{{y + 1}}{2} = \frac{{z + 1}}{1}.$
A. ${\left( {x – \frac{3}{2}} \right)^2} + {\left( {y + \frac{1}{2}} \right)^2} + {z^2} = \frac{3}{4}.$
B. ${\left( {x – \frac{3}{2}} \right)^2} + {\left( {y – \frac{1}{2}} \right)^2} + {z^2} = \frac{3}{2}.$
C. ${\left( {x – \frac{3}{2}} \right)^2} + {\left( {y + \frac{1}{2}} \right)^2} + {z^2} = \frac{3}{2}.$
D. ${(x – 1)^2} + {(y – 2)^2} + {(z + 1)^2} = \frac{3}{4}.$
Câu 5: Trong không gian với hệ tọa độ $Oxyz$, gọi $M$, $N$ là các điểm bất kì lần lượt thuộc $\Delta :\frac{{x – 1}}{2} = \frac{y}{1} = \frac{{z + 4}}{{ – 1}}$ và trục $Oy.$ Tính độ dài ngắn nhất của đoạn thẳng $MN.$
A. $2\sqrt 3 .$
B. $\frac{{7\sqrt 5 }}{5}.$
C. $4\sqrt 3 .$
D. $\frac{{2\sqrt 5 }}{5}.$
Câu 6: Trong không gian với hệ tọa độ $Oxyz$, tính khoảng cách $d$ từ giữa hai đường thẳng $\Delta :\frac{{x + 1}}{1} = \frac{y}{{ – 2}} = \frac{{z + 2}}{2}$ và trục $Oz.$
A. $d = \frac{{3\sqrt 5 }}{5}.$
B. $d = \frac{{3\sqrt 3 }}{2}.$
C. $d = \frac{{7\sqrt 5 }}{5}.$
D. $d = \frac{{2\sqrt 5 }}{5}.$
Câu 7: Trong không gian với hệ tọa độ $Oxyz$, cho tứ diện $ABCD$ với $A(1;1;2)$, $B(-3;3;4)$, $C(0;2;2)$, $D(0;1;-1).$ Tính khoảng cách $d$ giữa hai đường thẳng $AC$ và $BD.$
A. $d = \frac{{2\sqrt {11} }}{{11}}.$
B. $d = \frac{{\sqrt {51} }}{{51}}.$
C. $d = \frac{{8\sqrt {51} }}{{51}}.$
D. $d = \frac{{2\sqrt {15} }}{{11}}.$
Câu 8: Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình chữ nhật với $AB=1$, $AD=2$, $SA$ vuông góc với đáy và $SA=2.$ Gọi $M$, $N$ lần lượt là trung điểm của các cạnh $SD$, $BC$, tính khoảng cách $d$ giữa hai đường thẳng $CM$ và $AN.$
A. $d = \frac{{2\sqrt 6 }}{3}.$
B. $d = \frac{{\sqrt 6 }}{3}.$
C. $d = \frac{{\sqrt 6 }}{6}.$
D. $d = \frac{{\sqrt 2 }}{2}.$
Câu 9: Trong không gian với hệ tọa độ $Oxyz$, tính khoảng cách $d$ từ giữa đường thẳng $\Delta :\frac{{x + 1}}{{ – 1}} = \frac{{y + 2}}{{ – 1}} = \frac{{z + 1}}{1}$ và mặt phẳng $(P):x + y + 2z + 3 = 0.$
A. $d = \sqrt 3 .$
B. $d = \frac{1}{3}.$
C. $d = \frac{{\sqrt 6 }}{3}.$
D. $d = \frac{2}{3}.$
Câu 10: Trong không gian với hệ tọa độ $Oxyz$, gọi $M$, $N$ là các điểm bất kì lần lượt thuộc $\Delta :\frac{{x + 1}}{{ – 1}} = \frac{{y + 2}}{{ – 1}} = \frac{{z + 1}}{1}$ và mặt phẳng $(P):x + y + 2z + 3 = 0.$ Tính độ dài nhỏ nhất của đoạn thẳng $MN.$
A. $d = \sqrt 3 .$
B. $d = \frac{1}{3}.$
C. $d = \frac{{\sqrt 6 }}{3}.$
D. $d = \frac{2}{3}.$
2. BẢNG ĐÁP ÁN
| Câu | 1 | 2 | 3 | 4 | 5 |
| Đáp án | D | A | B | C | B |
| Câu | 6 | 7 | 8 | 9 | 10 |
| Đáp án | C | C | D | C | C |









