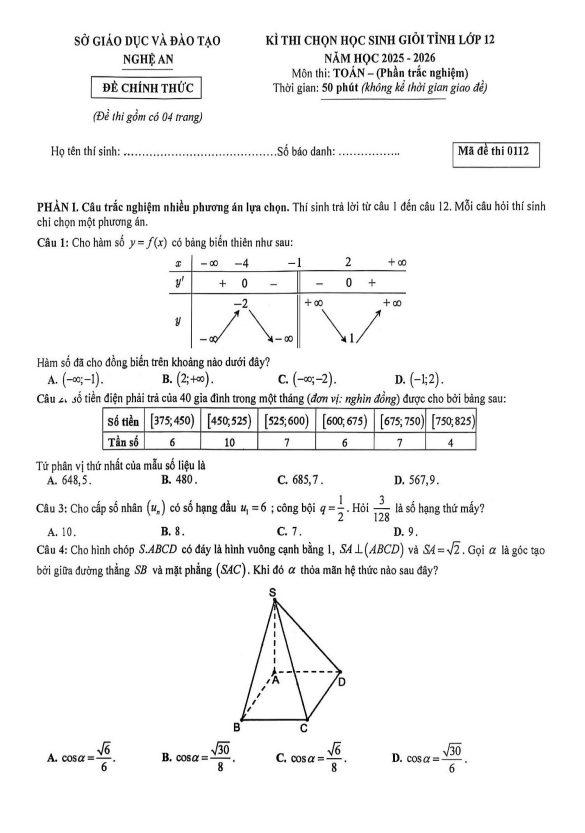
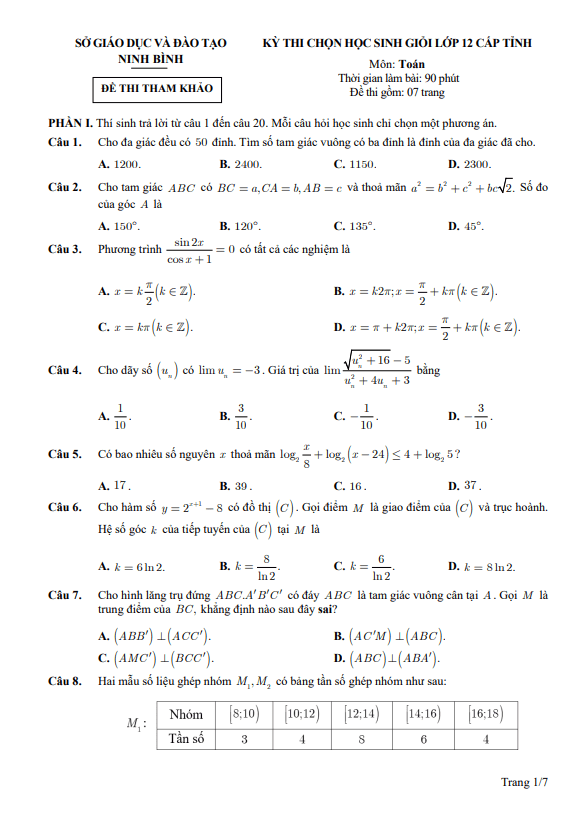TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh đề thi chọn học sinh giỏi Quốc gia môn Toán THPT năm học 2024 – 2025. Kỳ thi được diễn ra vào ngày 25/12/2024 và 26/12/2024. Đề thi có đáp án và lời giải chi tiết.
Trích dẫn Đề thi chọn học sinh giỏi Quốc gia môn Toán THPT năm học 2024 – 2025:
+ Cho một bảng ô vuông 3k × 3k (k là số nguyên dương), các ô của bảng được đánh tọa độ theo cột và hàng: ô (i; j) nằm trên cột thứ i từ trái qua phải và trên hàng thứ j từ dưới lên trên. Người ta muốn đặt 4k viên bi vào các ô của bảng, mỗi ô có không quá một viên, thỏa mãn đồng thời hai điều kiện sau: Mỗi hàng và mỗi cột đều có ít nhất một viên bi; Mỗi viên bi nằm cùng hàng hoặc cùng cột với ít nhất một viên bi khác. a) Xét k = 1. Có bao nhiêu cách đặt 4 viên bi vào bảng thỏa mãn các điều kiện trên? (Hai cách đặt bi được coi là khác nhau nếu có một ô (i; j) có bi trong một cách đặt nhưng không có bi trong cách còn lại). a) Xét k > 1 tổng quát. Xác định số tự nhiên N lớn nhất sao cho với mọi cách đánh dấu N ô phân biệt trên bảng, luôn tồn tại một cách đặt 4k viên bi thỏa mãn các điều kiện trên mà không có viên bi nào đặt ở một trong N ô đã được đánh dấu.
+ Xét đa thức P(x) = x4 − x3 + x. a) Chứng minh rằng với mọi số dương a, đa thức P(x) − a có duy nhất một nghiệm dương. b) Xét dãy số (an) được xác định bởi a1 = 1/3 và với mọi n > 1, an+1 là nghiệm dương của đa thức P(x) − an. Chứng minh rằng dãy (an) có giới hạn hữu hạn và tìm giới hạn đó.
+ Với mỗi số nguyên n > 0, đặt un = (2 + √5)^n + (2 − √5)^n. a) Chứng minh rằng un là số nguyên dương với mọi n > 0. Khi n thay đổi, số dư của un khi chia cho 24 lớn nhất bằng bao nhiêu? b) Tìm tất cả các cặp số nguyên dương (a, b) với a, b nhỏ hơn 500 sao cho với mọi n lẻ ta có un ≡ an − bn (mod 1111).