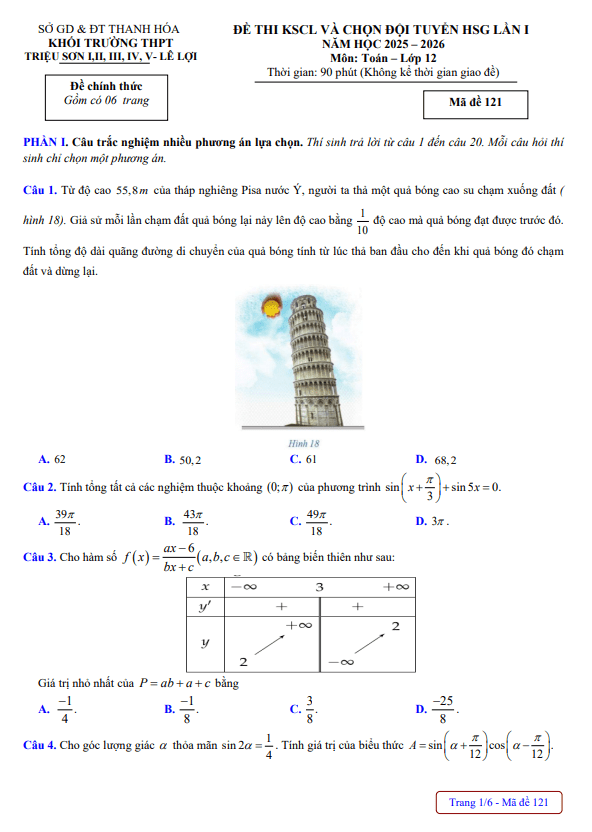
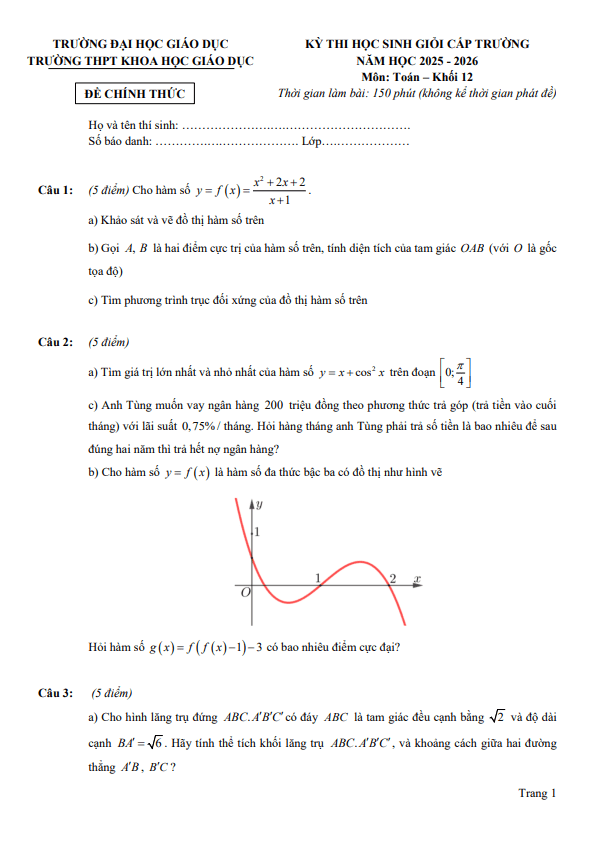
TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh đề chính thức kỳ thi chọn học sinh giỏi môn Toán THPT cấp thành phố năm học 2025 – 2026 sở Giáo dục và Đào tạo thành phố Huế. Đề thi gồm 12 câu trắc nghiệm nhiều phương án lựa chọn (3,0 điểm) + 04 câu trắc nghiệm đúng sai (4,0 điểm) + 06 câu trắc nghiệm trả lời ngắn (3,0 điểm) + 05 câu tự luận (10,0 điểm), thời gian làm bài 150 phút. Kỳ thi được diễn ra vào tháng 10 năm 2025.
Trích dẫn Đề chọn học sinh giỏi Toán THPT năm 2025 – 2026 sở GD&ĐT Huế:
+ Hai bạn An và Bình cùng chơi một số ván cờ Caro, biết rằng trong mỗi ván luôn có một người thắng. Người thua ở ván này sẽ được đi trước ở ván tiếp theo. Người thắng cuộc là người thắng được 2 ván trước người kia. Biết rằng nếu An đi trước thì xác suất An thắng ván đó là 0,9 và nếu Bình đi trước thì xác suất Bình thắng ván đó là 0,7. Giả sử An đi trước ở ván đầu tiên, tính xác suất để An là người thắng cuộc (kết quả làm tròn đến hàng phần trăm).
+ Tại một góc vườn của ông Bình, hai bức tường rào tạo với nhau một góc 60°. Ông ấy muốn dùng một tấm lưới dài 10 m, kết hợp với hai bức tường để làm một khu vực nuôi vịt có dạng hình thang vuông (xem hình minh họa, ông Bình cần giăng hết lưới tạo thành hai cạnh vuông góc AD và AB, các bức tường đều có độ dài lớn hơn 10 m). Tính diện tích lớn nhất của khu vực nuôi vịt đó (đơn vị là m2, kết quả làm tròn đến hàng phần chục).
+ Từ một hình vuông ABCD cạnh bằng 1, ta thực hiện như sau: Chia cạnh AB thành 3 đoạn bằng nhau, về phía ngoài, dựng hình vuông có cạnh là đoạn ở giữa rồi xóa đi đoạn đó, ta được hình H. Trên mỗi cạnh song song với CD của hình H, ta lại chia thành 3 đoạn bằng nhau, về phía ngoài, dựng hình vuông có cạnh là đoạn ở giữa và xóa đi đoạn đó, ta được hình H2. Ta tiếp tục lặp lại quá trình như trên. Gọi Sn là diện tích của hình Hn, tính lim Sn (kết quả làm tròn đến hàng phần trăm).