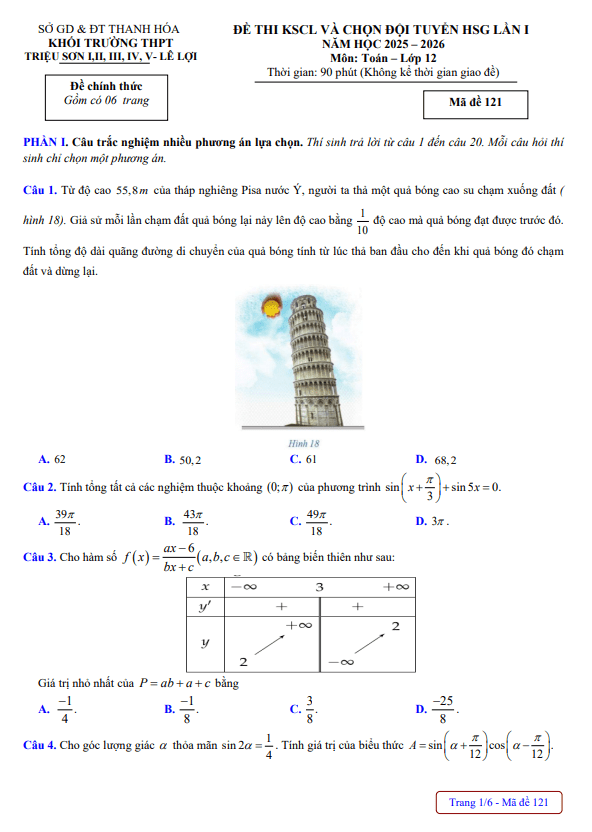
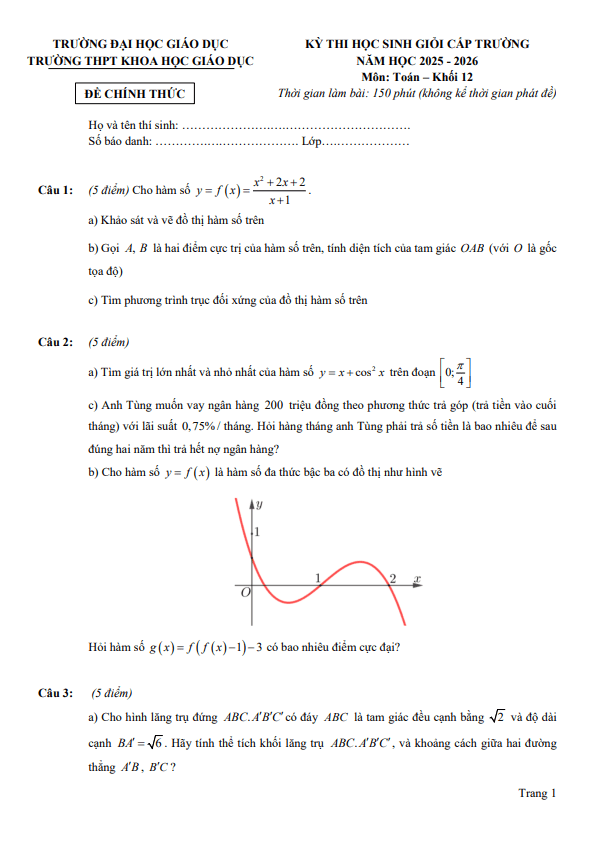
TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh đề thi chọn học sinh giỏi cấp tỉnh tham dự kỳ thi chọn học sinh giỏi Quốc gia môn Toán THPT năm học 2025 – 2026 sở Giáo dục và Đào tạo tỉnh Quảng Ngãi. Kỳ thi được diễn ra vào ngày 18 và ngày 19 tháng 09 năm 2025.
Trích dẫn Đề chọn HSG tỉnh dự thi QG môn Toán THPT năm 2025 – 2026 sở GD&ĐT Quảng Ngãi:
+ Cho một bảng ô vuông kích thước 999 × 999. a) Điền vào mỗi ô của bảng một số nguyên dương. Cho phép thay đổi số ở trong bảng, theo quy tắc: giảm bớt 1 đơn vị của số ghi trong mỗi ô ở một hàng tùy ý, mà ở tất cả các ô của hàng đó đều khác 0; hoặc gấp đôi số của mỗi ô ở một cột tùy ý. Chứng minh rằng ta có thể thực hiện hữu hạn lần phép thay đổi nói trên, để tất cả các số trong bảng giống nhau. b) Tô màu đen một số ô trong bảng sao cho trong mỗi bảng con 5 x 5 bất kỳ có ít nhất 8 ô được tô màu đen. Tìm số ô đen ít nhất có thể tô trên bảng ô vuông.
+ Cho đa thức P(x) với hệ số là số thực không âm và hàm số f thỏa mãn f(x + P(x)f(y)) = (y + 1)f(x) với mọi x, y ∈ R+. a) Chứng minh rằng hàm số f là một song ánh và là hàm số liên tục trên R+. b) Tìm tất cả các hàm số f và đa thức P(x) khác đa thức hằng thỏa mãn điều kiện trên và P(0) = 0.