Bài viết hướng dẫn phương pháp khảo sát sự biến thiên và vẽ đồ thị của một số hàm phân thức hữu tỉ thường gặp trong chương trình Giải tích 12.
A. TÓM TẮT SÁCH GIÁO KHOA
Các bước để khảo sát hàm số dạng phân thức hữu tỉ:
1) Tìm tập xác định.
2) Tìm các giới hạn và tiệm cận.
3) Xét chiều biến thiên:
+ Tìm $y’$. Giải phương trình $y’ = 0.$
+ Lập bảng biến thiên.
+ Suy ra các khoảng đơn điệu và các điểm cực trị.
4) Vẽ đồ thị:
+ Lấy các giá trị đặc biệt.
+ Vẽ các tiệm cận, các điểm đặc biệt và vẽ đồ thị hàm số.
+ Nhận xét đặc điểm của đồ thị.
B. PHƯƠNG PHÁP GIẢI TOÁN
Vấn đề 1: Khảo sát sự biến thiên và vẽ đồ thị hàm số dạng $y = \frac{{ax + b}}{{cx + d}}$ ($c \ne 0$ và $ad – bc \ne 0$).
1. PHƯƠNG PHÁP:
1. Tập xác định: $D = R\backslash \left\{ { – \frac{d}{c}} \right\}.$
2. Giới hạn và tiệm cận:
+ Tiệm cận đứng: $x = – \frac{d}{c}.$
+ Tiệm cận ngang: $y = \frac{a}{c}.$
3. Khảo sát sự biến thiên:
$y’ = \frac{{ad – bc}}{{{{(cx + d)}^2}}}$. Dấu $y’$ là dấu của hằng số $T = ad – bc.$
$T > 0$: Hàm số tăng trên từng khoảng xác định.
$T < 0$: Hàm số giảm trên từng khoảng xác định.
Hàm số không có cực trị.
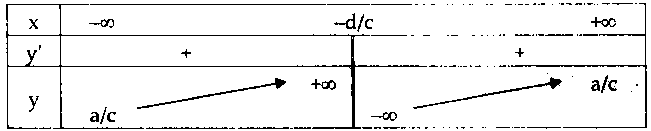
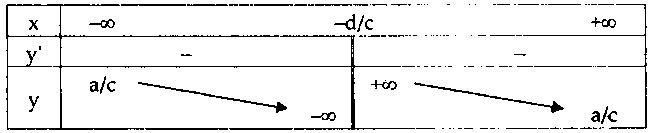
Bảng biến thiên có 2 dạng sau:
$ad – bc > 0.$
$ad – bc < 0.$
4. Đồ thị:
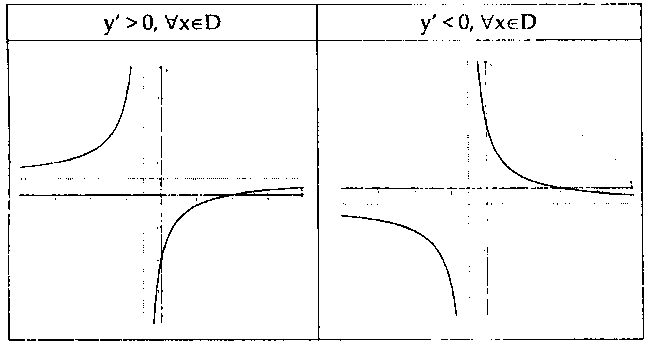
Nhận xét: Đồ thị nhận giao điểm $I\left( { – \frac{d}{c};\frac{a}{c}} \right)$ của hai tiệm cận làm tâm đối xứng.
2. CÁC VÍ DỤ:
Ví dụ 1: Khảo sát sự biến thiên và vẽ đồ thị của hàm số: $y = \frac{{x – 3}}{{x + 1}}.$
1. Tập xác định: $D = R\backslash \left\{ { – 1} \right\}.$
2. Khảo sát sự biến thiên:
$\left\{ {\begin{array}{*{20}{l}}
{\mathop {\lim }\limits_{x \to – {1^ – }} y = \mathop {\lim }\limits_{x \to – {1^ – }} \frac{{x – 3}}{{x + 1}} = + \infty }\\
{\mathop {\lim }\limits_{x \to – {1^ + }} y = \mathop {\lim }\limits_{x \to – {1^ + }} \frac{{x – 3}}{{x + 1}} = – \infty }
\end{array}} \right.$ $ \Rightarrow x = – 1$ là tiệm cận đứng của đồ thị hàm số.
$\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{x – 3}}{{x + 1}} = 1$ $ \Rightarrow y = 1$ là tiệm cận ngang của đồ thị hàm số.
$y’ = \frac{4}{{{{(x + 1)}^2}}} > 0$, $\forall x \in D.$
Suy ra hàm số đồng biến trên các khoảng xác định.
Bảng biến thiên:
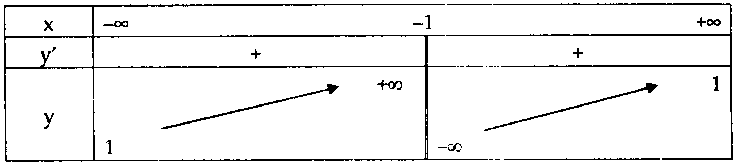
Hàm số không có cực trị.
Giá trị đặc biệt:
![]()
Đồ thị:

Nhận xét: Đồ thị $(C)$ nhận giao điểm $I(-1;-1)$ của hai tiệm cận làm tâm đối xứng.
Ví dụ 2:
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số $y = \frac{{2x + 1}}{{x – 1}}.$
b) Chứng minh đồ thị $(C)$ nhận giao điểm của hai tiệm cận làm tâm đối xứng.
a) Khảo sát hàm số:
1. Tập xác định: $D = R\backslash \{ 1\} .$
2. Khảo sát sự biến thiên:
Giới hạn và tiệm cận:
$\left\{ {\begin{array}{*{20}{l}}
{\mathop {\lim }\limits_{x \to {1^ – }} y = + \infty }\\
{\mathop {\lim }\limits_{x \to {1^ + }} y = – \infty }
\end{array}} \right.$ $ \Rightarrow x = 1$ là tiệm cận đứng của đồ thị.
$\mathop {\lim }\limits_{x \to \pm \infty } y = \mathop {\lim }\limits_{x \to \pm \infty } \frac{{2x + 1}}{{x – 1}} = 2$ $ \Rightarrow y = 2$ là tiệm cận ngang của đồ thị hàm số.
Sự biến thiên: $y’ = \frac{{ – 3}}{{{{(x – 1)}^2}}} < 0$, $\forall x \in D.$
Suy ra hàm số nghịch biến trên các khoảng xác định.
Bảng biến thiên:

Hàm số không có cực trị.
Giá trị đặc biệt:
![]()
Đồ thị:
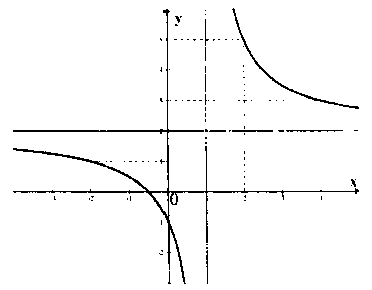
Nhận xét: Đồ thị $(C)$ nhận giao điểm $I(1;2)$ của hai tiệm cận làm tâm đối xứng.
b) Chứng minh đồ thị $(C)$ nhận giao điểm hai tiệm cận làm tâm đối xứng.
Tịnh tiến hệ trục $Oxy$ về hệ trục $IXY.$ Công thức chuyển hệ trục là:
$\left\{ {\begin{array}{*{20}{l}}
{x = X + 1}\\
{y = Y + 2}
\end{array}} \right. .$
Đối với hệ trục $IXY$ thì đồ thị $(C)$ có phương trình:
$Y + 2 = \frac{{2(X + 1) + 1}}{{X + 1 – 1}}$ $ \Leftrightarrow Y = \frac{3}{X} = F(X).$
Ta có: $F(X)$ có tập xác định là ${D_F} = R\backslash \{ 0\} $ nên $X \in {D_F}$ thì $ – X \in {D_F}.$
$F( – X) = – \frac{3}{X} = – F(X).$
Vậy $F(X)$ là hàm số lẻ. Suy ra đồ thị $(C)$ nhận $I$ làm tâm đối xứng.
3. BÀI TẬP:
1. Khảo sát sự biến thiên và vẽ đồ thị của các hàm số:
a) $y = \frac{{2x – 1}}{{x + 2}}.$
b) $y = \frac{{2x + 3}}{{x – 1}}.$
2. Cho hàm số $y = \frac{{ – mx – 5m – 2}}{{x – 2m}}.$
a) Định $m$ để hàm số tăng trong các khoảng xác định.
b) Khảo sát và vẽ đồ thị $(C)$ của hàm số khi $m = -1.$
c) Tìm hai điểm $M$, $N$ lần lượt thuộc hai nhánh của $(C)$ sao cho độ dài của đoạn $MN$ nhỏ nhất.
d) Viết phương trình đường thẳng $(d)$, biết $(d)$ tiếp xúc $(C)$ tại $M$ và $(d)$ vuông góc với $IM$ ($I$ là giao điểm hai tiệm cận của $(C)$).
3.
a) Khảo sát sự biến thiên và vẽ đồ thị $(H)$ của hàm số $y = \frac{{3x – 1}}{{x – 2}}.$
b) Tìm những điểm trên $(H)$ có tọa độ nguyên.
c) Cho điểm $M$ tùy ý thuộc $(H).$ Chứng minh tích các khoảng cách từ $M$ đến hai tiệm cận của $(H)$ là hằng số.
4.
a) Khảo sát và vẽ đồ thị $(C)$ của hàm số $y = \frac{{x + 2}}{{2x – 2}}.$
b) Tìm trên $(C)$ những điểm cách đều hai trục tọa độ.
c) Viết phương trình tiếp tuyến của $(C)$ biết tiếp tuyến song song với đường thẳng $(\Delta ):y = – \frac{3}{2}x + 10.$
5. Cho hàm số $y = \frac{{x + 1}}{{x – 3}}.$
a) Khảo sát và vẽ đồ thị $(C)$ của hàm số.
b) Chứng minh giao điểm $I$ của hai tiệm cận là tâm đối xứng của $(C).$
c) Tìm những điểm $M$ trên $(C)$ sao cho khoảng cách từ $M$ đến tiệm cận đứng bằng bốn lần khoảng cách từ $M$ đến tiệm cận ngang.
6. Cho hàm số $y = \frac{{x + 2}}{{2x + 3}}.$
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
b) Viết phương trình tiếp tuyến của đồ thị hàm số, biết tiếp tuyến đó cắt trục hoành, trục tung lần lượt tại hai điểm phân biệt $A$, $B$ và tam giác $OAB$ cân tại gốc tọa độ $O.$
Vấn đề 2: Khảo sát sự biến thiên và vẽ đồ thị hàm số dạng $y = \frac{{a{x^2} + bx + c}}{{mx + n}}.$
I. PHƯƠNG PHÁP:
Hàm số $y = \frac{{a{x^2} + bx + c}}{{mx + n}}$ ($am \ne 0$, $ – \frac{n}{m}$ không là nghiệm của tử số).
1. Tập xác định: $D = R\backslash \left\{ { – \frac{n}{m}} \right\}.$
2. Giới hạn và tiệm cận
Tiệm cận đứng: $x = – \frac{n}{m}.$
$y = Ax + B + \frac{C}{{mx + n}}$ suy ra tiệm cận xiên $y = Ax + B.$
3. Khảo sát sự biến thiên
$y’ = \frac{{am{x^2} + 2anx + bn – cm}}{{{{(mx + n)}^2}}}.$
Dấu $y’$ là dấu của $g(x) = am{x^2} + 2anx + bn – cm.$
${\Delta _g} > 0$: Hàm số có $2$ cực trị.
${\Delta _g} \le 0$: Hàm số không có cực trị.
Bảng biến thiên:
+ Hàm số có $2$ cực trị và $a.m > 0.$
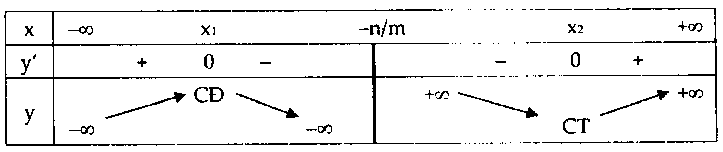
+ Hàm số có $2$ cực trị và $a.m< 0.$

+ Hàm số không có cực trị và $a.m > 0.$

+ Hàm số không có cực trị và $a.m < 0.$

4. Đồ thị
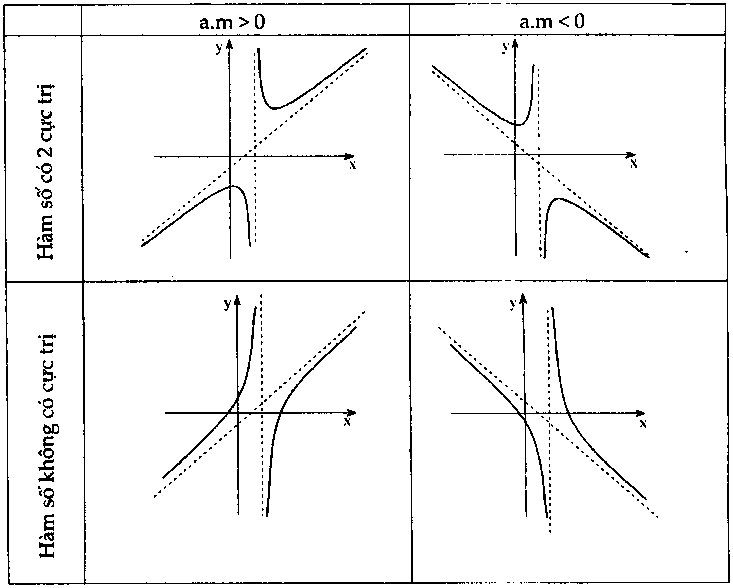
Nhận xét: Đồ thị nhận giao điểm của hai tiệm cận làm tâm đối xứng.
II. CÁC VÍ DỤ:
Ví dụ 1: Khảo sát sự biến thiên và vẽ đồ thị của hàm số: $y = \frac{{2{x^2}}}{{x + 1}}.$
Ta có: $y = \frac{{2{x^2}}}{{x + 1}} = 2x – 2 + \frac{2}{{x + 1}}.$
Tập xác định: $D = R\backslash \{ – 1\} .$
Giới hạn và tiệm cận:
$\left\{ {\begin{array}{*{20}{c}}
{\mathop {\lim }\limits_{x \to – {1^ – }} y = – \infty }\\
{\mathop {\lim }\limits_{x \to – {1^ + }} y = + \infty }
\end{array}} \right.$ $ \Rightarrow x = – 1$ là tiệm cận đứng của đồ thị.
$\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y – (2x – 2)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } \frac{2}{{x + 1}} = 0$ $ \Rightarrow y = 2x – 2$ là tiệm cận xiên của đồ thị.
Sự biến thiên: $y’ = \frac{{2{x^2} + 4x}}{{{{(x + 1)}^2}}}$, $y’ = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0 \Rightarrow y = 0}\\
{x = – 2 \Rightarrow y = – 8}
\end{array}} \right..$
Bảng biến thiên:
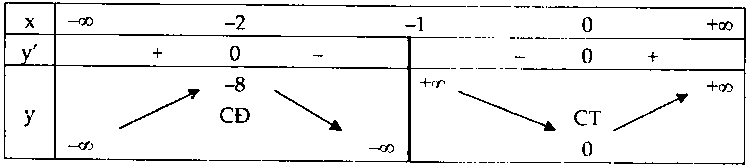
Hàm số tăng trong $( – \infty ; – 2)$ và $(0; + \infty )$, giảm trong $( – 2; – 1)$ và $( – 1;0).$
Hàm số đạt cực đại tại $x = – 2$ và ${y_{CĐ}} = – 8$, đạt cực tiểu tại $x = 0$ và ${y_{CT}} = 0.$
Giá trị đặc biệt:

Đồ thị:

Nhận xét: Đồ thị nhận giao điểm $I(-1;-3)$ của hai tiệm cận làm tâm đối xứng.
Ví dụ 2: Khảo sát sự biến thiên và vẽ đồ thị của hàm số $y = – x + 1 + \frac{1}{{x – 1}}.$
Ta có $y = – x + 1 + \frac{1}{{x – 1}} = \frac{{ – {x^2} + 2x}}{{x – 1}}.$
Tập xác định: $D = R\backslash \{ 1\} .$
Giới hạn và tiệm cận:
$\left\{ {\begin{array}{*{20}{l}}
{\mathop {\lim }\limits_{x \to {1^ – }} y = \mathop {\lim }\limits_{x \to {1^ – }} \frac{{ – {x^2} + 2x}}{{x – 1}} = – \infty }\\
{\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{ – {x^2} + 2x}}{{x – 1}} = + \infty }
\end{array}} \right.$ $ \Rightarrow x = 1$ là tiệm cận đứng của đồ thị.
$\mathop {\lim }\limits_{x \to \pm \infty } [y – ( – x + 1)]$ $ = \mathop {\lim }\limits_{x \to \pm \infty } \frac{1}{{x – 1}} = 0$ $ \Rightarrow y = – x + 1$ là tiệm cận xiên của đồ thị.
Sự biến thiên: $y’ = \frac{{ – {x^2} + 2x – 2}}{{{{(x + 1)}^2}}}$, $y’ = 0$ $ \Leftrightarrow – {x^2} + 2x – 2 = 0$ $ \Leftrightarrow x \in \emptyset .$
Bảng biến thiên:
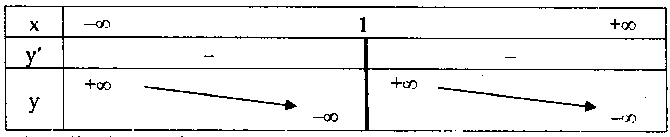
Hàm số nghịch biến trong $( – \infty ;1)$ và $(1; + \infty ).$ Hàm số không có cực trị.
Giá trị đặc biệt:

Đồ thị:
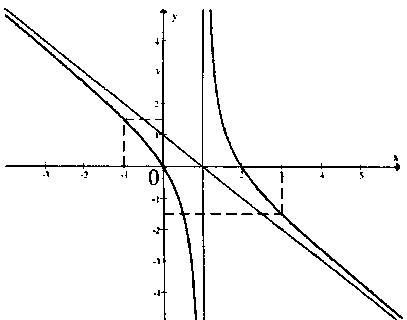
Nhận xét: Đồ thị nhận giao điểm $I(1;1)$ của hai tiệm cận làm tâm đối xứng.
III. BÀI TẬP:
1. Cho hàm số $y = \frac{{{x^2} – 2mx + 3{m^2} – 3}}{{x – 2m}}.$
a) Định $m$ để hàm số đồng biến trên các khoảng xác định.
b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi $m = 2.$
2. Cho hàm số $y = \frac{{{x^2} – x – 1}}{{2 – x}}.$
a) Khảo sát sự biến thiên và vẽ đồ thị $(C)$ của hàm số.
b) Tìm điểm trên $(C)$ có tọa độ nguyên.
c) Tìm điểm trên $(C)$ cách đều hai trục tọa độ.
3. Cho hàm số $y = \frac{{{x^2} + (2m + 3)x + {m^2} + 4m}}{{x + m}}$ $\left( {{H_m}} \right).$
a) Khảo sát và vẽ đồ thị $(C)$ của hàm số khi $m= -1.$
b) Tìm $m$ để hàm số có $2$ cực trị và $2$ giá trị cực trị trái dấu nhau.
4. Cho hàm số $y = \frac{{{x^2} – x + 1}}{{x – 1}}.$
a) Khảo sát và vẽ đồ thị $(C)$ của hàm số.
b) Tìm hai điểm $A$, $B$ thuộc hai nhánh khác nhau của $(C)$ sao cho $AB$ nhỏ nhất.
5. Cho hàm số $y = \frac{{{x^2} – (m + 1)x – {m^2} + 4m – 2}}{{x – 1}}.$
a) Định $m$ để hàm số có cực trị. Tìm $m$ để tích các giá trị cực trị đạt giá trị nhỏ nhất.
b) Khảo sát và vẽ đồ thị $(C)$ của hàm số khi $m = 0.$
c) Tìm các điểm nguyên trên đồ thị $(C).$
6. Cho hàm số $y = \frac{{{x^2} + (m + 1)x – m + 1}}{{x – m}}.$
a) Khảo sát và vẽ đồ thị $(C)$ của hàm số khi $m = 2.$
b) Chứng minh rằng tích các khoảng cách từ điểm $M$ tuỳ ý thuộc $(C)$ đến hai tiệm cận là một hằng số.
c) Định $m$ để hàm số có cực trị và $2$ giá trị cực trị cùng dấu.
7. Cho hàm số $y = x – \frac{1}{{x + 1}}.$
a) Khảo sát và vẽ đồ thị $(C)$ của hàm số.
b) Tìm $m$ để đường thẳng $y = m$ cắt $(C)$ tại hai điểm $A$, $B$ sao cho $OA$ vuông góc $OB.$
8. Cho hàm số $y = \frac{{{x^2} – (m + 1)x + 4{m^2} – 4m}}{{x – m + 1}}.$
a) Khảo sát và vẽ đồ thị $(C)$ của hàm số khi $m=2.$
b) Định $m$ để hàm số xác định và luôn tăng trong khoảng $(0, + \infty ).$
9. Cho $y = \frac{{{x^2} + mx – 1}}{{x – 1}}.$
a) Khảo sát hàm số khi $m=1.$
b) Tìm các giá trị $m$ để tiệm cận xiên của đồ thị hàm số cắt hai trục tọa độ tại hai điểm $A$, $B$ sao cho ${S_{OAB}} = 18.$









