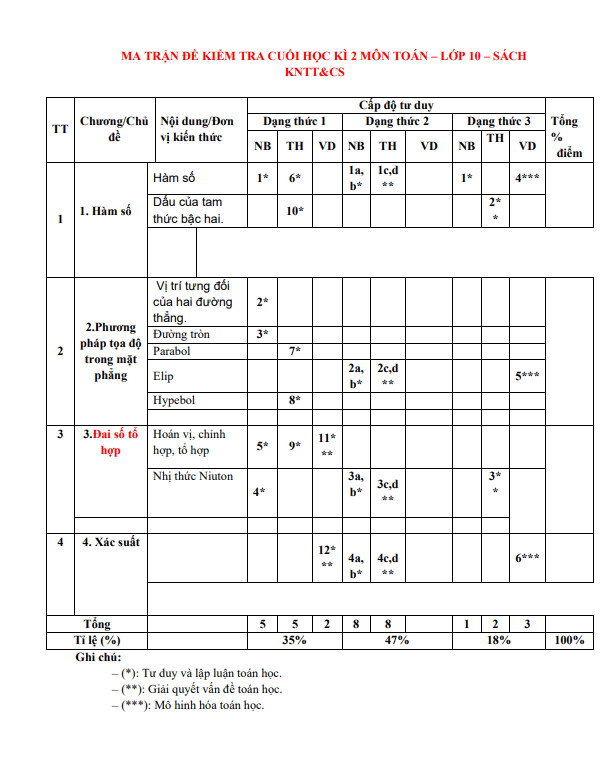
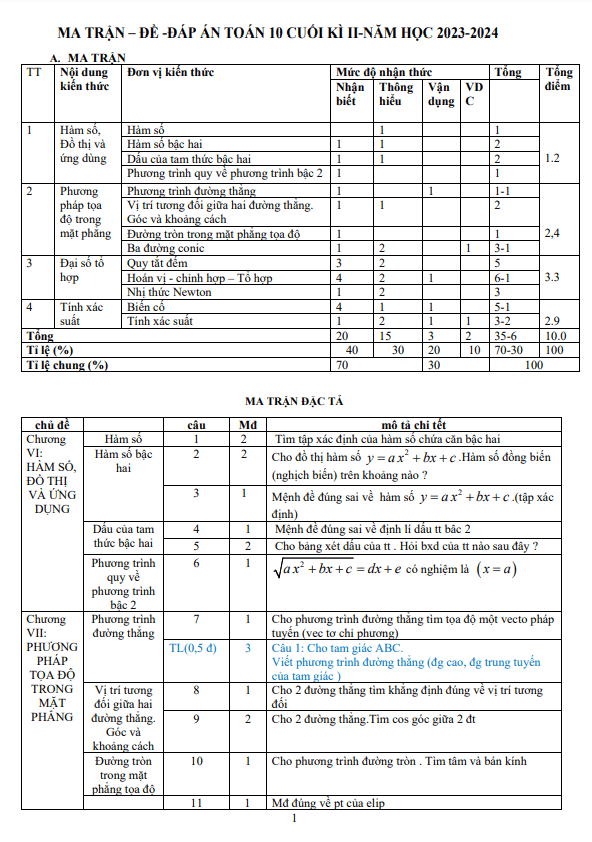
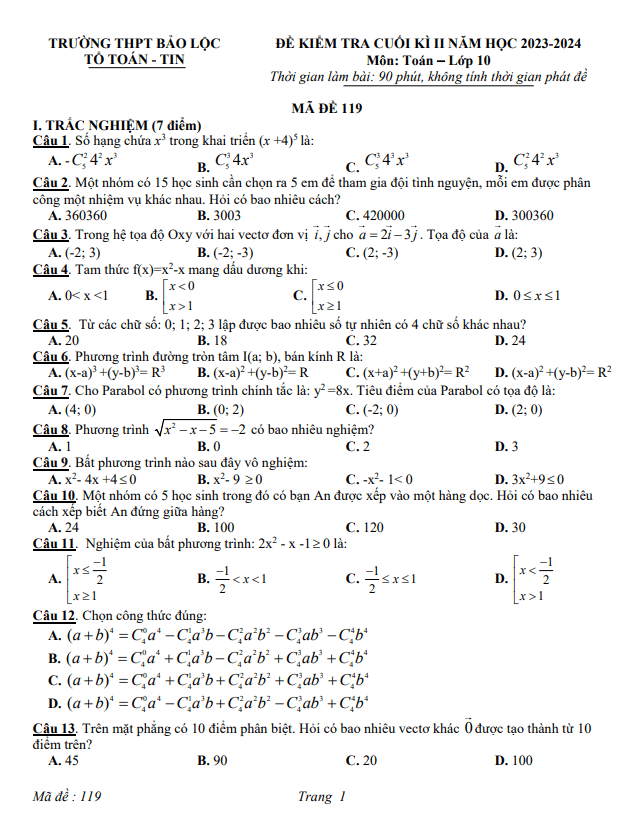TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề minh họa kiểm tra cuối học kì 2 môn Toán 10 năm học 2023 – 2024 sở Giáo dục và Đào tạo tỉnh Quảng Ngãi; đề thi được biên soạn theo cấu trúc 70% trắc nghiệm + 30% tự luận (theo điểm số), có ma trận, bảng đặc tả, đáp án và hướng dẫn chấm điểm.
1 BẤT PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
1.1. Dấu của tam thức bậc hai.
– Nhận biết:
+ Nhận biết được dấu của tam thức bậc hai trong trường hợp đặc biệt.
+ Tính được nghiệm và biệt thức của tam thức bậc hai.
– Thông hiểu:
+ Hiểu được định về dấu của tam thức bậc hai.
1.2. Giải BPT bậc hai một ẩn.
– Nhận biết:
+ Nhận biết được bất phương trình bậc hai một ẩn.
– Thông hiểu:
+ Giải được bất phương trình bậc hai một ẩn.
+ Hiểu được định lý về dấu của tam thức bậc hai trong bất phương trình bậc hai.
1.3. Phương trình quy về phương trình bậc hai.
– Nhận biết:
+ Nhận biết nghiệm phương trình.
– Thông hiểu:
+ Giải phương trình.
2 PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
2.2. Đường thẳng trong mp tọa độ.
– Nhận biết:
+ Nhận biết được phương trình tổng quát và phương trình tham số của đường thẳng trong mặt phẳng tọa độ; VT chỉ phương, VT pháp tuyến.
+ Biết công thức tính góc giữa 2 đường thẳng, công thức tính khoảng cách từ điểm đến đường thẳng.
– Thông hiểu:
+ Viết phương trình tham số, phương trình tổng quát của đường thẳng trường hợp đơn giản.
+ Xác định được hai đường thẳng cắt nhau, song song, trùng nhau, vuông góc với nhau bằng phương pháp tọa độ.
+ Tính được khoảng cách từ một điểm đến một đường thẳng bằng phương pháp tọa độ.
– Vận dụng:
+ Viết phương trình tham số, phương trình tổng quát của đường thẳng thoả điều kiện cho trước.
– Vận dụng cao:
+ Vận dụng được kiến thức về phương trình đường thẳng để giải một số bài toán có liên quan đến thực tiễn.
2.3. Đường tròn trong mp tọa độ.
– Nhận biết:
+ Nhận dạng được phương trình đường tròn trong mặt phẳng tọa độ.
– Thông hiểu:
+ Viết được phương trình đường tròn khi biết tọa độ tâm và bán kính; biết tọa độ ba điểm mà đường tròn đi qua; xác định được tâm và bán kính đường tròn khi biết phương trình của đường tròn.
– Vận dụng:
+ Viết được phương trình tiếp tuyến của đường tròn khi biết tọa độ của tiếp điểm.
– Vận dụng cao:
+ Vận dụng được kiến thức về phương trình đường tròn để giải một số bài toán liên quan đến thực tiễn (ví dụ: bài toán về chuyển động tròn trong Vật lí).
2.4. Ba đường Conic trong mp tọa độ.
– Nhận biết:
+ Nhận biết được tiêu điểm các đường conic bằng hình học.
+ Nhận biết được phương trình chính tắc của các đường conic trong mặt phẳng tọa độ.
– Thông hiểu:
+ Tìm các yếu tố của các đường conic.
3 ĐẠI SỐ TỔ HỢP
3.1. Quy tắc cộng và quy tắc nhân.
– Nhận biết:
+ Nhận biết quy tắc cộng và quy tắc nhân.
– Thông hiểu:
+ Vẽ và sử dụng được sơ đồ hình cây trong mô tả, trình bày, giải thích khi giải các bài toán đơn giản.
– Vận dụng cao:
+ Vận dụng được quy tắc cộng và quy tắc nhân trong một số tình huống đơn giản (ví dụ: đếm số khả năng xuất hiện mặt sấp / ngửa khi tung một số đồng xu).
+ Vận dụng được sơ đồ hình cây trong các bài toán đếm đơn giản các đối tượng trong Toán học, trong các môn học khác cũng như trong thực tiễn (ví dụ: đếm số hợp tử tạo thành trong Sinh học, hoặc đếm số trận đấu trong một giải thể thao).
3.2. Hoán vị, chỉnh hợp và tổ hợp.
– Nhận biết:
+ Nhận biết các khái niệm hoán vị, chỉnh hợp và tổ hợp.
+ Nhận biết được các hoán vị, chỉnh hợp, tổ hợp trong những tình huống thực tế đơn giản.
– Thông hiểu:
+ Tính được số các hoán vị, chỉnh hợp, tổ hợp.
– Vận dụng:
+ Vận dụng được khái niệm hoán vị, chỉnh hợp, tổ hợp để giải những bài toán đếm trong tình huống thực tế.
+ Vận dụng được khái niệm hoán vị, chỉnh hợp, tổ hợp để giải những bài toán tìm số.
3.3. Nhị thức Newton.
– Nhận biết:
+ Nhận biết được số hạng, số hạng của công thức khai triển nhị thức Newton.
– Thông hiểu:
+ Sử dụng các công thức này khai triển các nhị thức Newton với số mũ thấp.
4 XÁC SUẤT
4.1. Không gian mẫu và biến cố.
– Nhận biết:
+ Biết khái niệm không gian mẫu, biến cố.
– Thông hiểu:
+ Mô tả được không gian mẫu, biến cố trong một số thí nghiệm đơn giản.
4.2. Xác suất của biến cố.
– Nhận biết:
+ Biết tính xác suất của biến cố đơn giản.
+ Nhận biết được biến cố đối và tính được xác suất của biến cố đối.
– Thông hiểu:
+ Mô tả được tính chất cơ bản của xác suất và tính xác suất của biến cố.
– Vận dụng:
+ Tính được xác suất trong một số thí nghiệm lặp bằng cách sử dụng sơ đồ hình cây.
+ Tính được xác suất của biến cố trong bài toán thực tế.
File WORD (dành cho quý thầy, cô): TẢI XUỐNG