TOANMATH.com giới thiệu đến quý thầy, cô giáo và các em học sinh tài liệu chuyên đề đường thẳng và mặt phẳng trong không gian, quan hệ song song do thầy Lư Sĩ Pháp biên soạn, tài liệu gồm 54 trang tổng hợp các kiến thức cần nắm, phân dạng bài tập và hướng dẫn giải các dạng toán thuộc chương trình Hình học 11 chương 2, tài liệu được soạn theo hướng tự luận kết hợp với trắc nghiệm, phần tự luận được phân tích và giải chi tiết nhằm giúp học sinh nắm được kỹ thuật giải toán, phần trắc nghiệm có đáp án giúp học sinh rèn luyện, phù hợp với xu hướng kiểm tra – thi cử hiện hành.
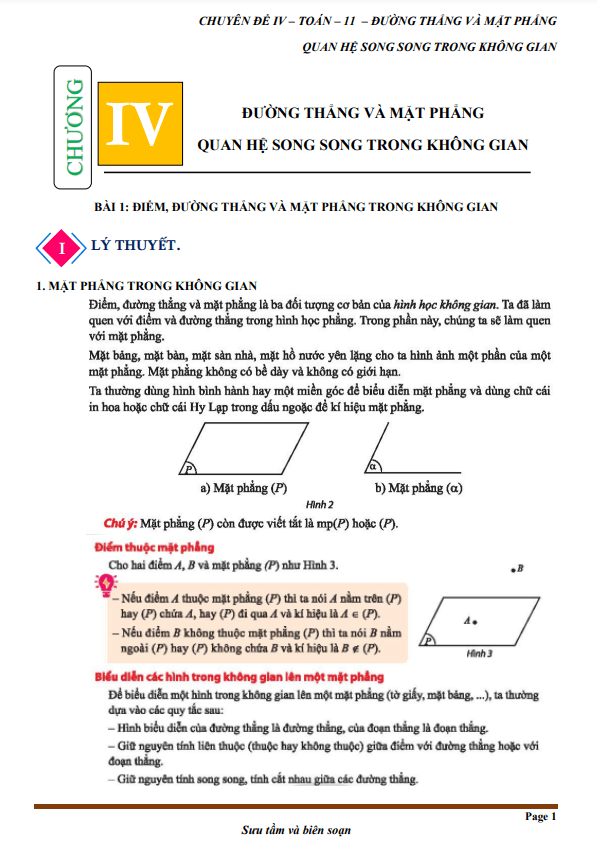
§1. ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG
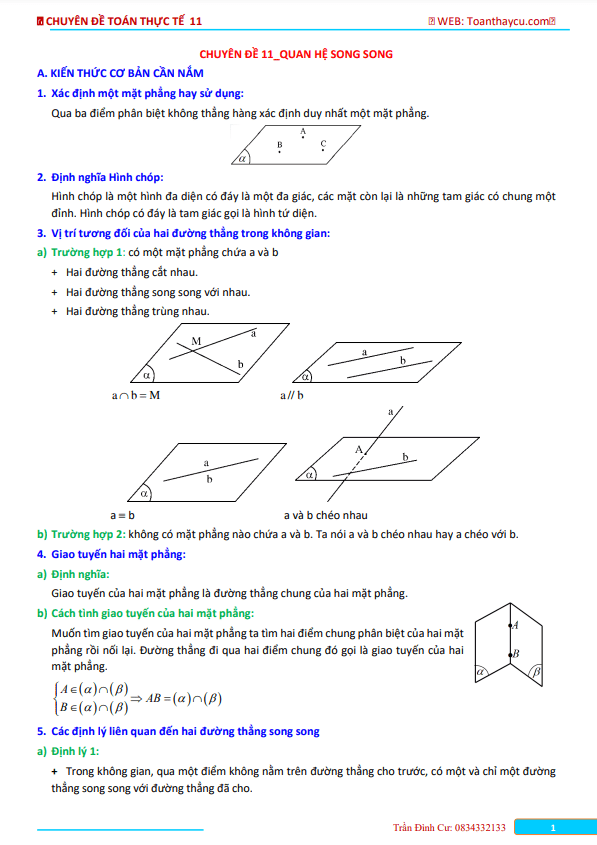
Vấn đề 1. Tìm giao tuyến của hai mặt phẳng: Ta đi tìm hai điểm chung phân bệt của hai mặt phẳng đó. Giao tuyến của chúng là đường thẳng đi qua hai điểm đó.
Vấn đề 2. Tìm giao điểm của đường thẳng d và mặt phẳng (α): Để tìm giao điểm của một đường thẳng d và một mặt phẳng (α), ta có thể đưa về việc tìm giao điểm của đường thẳng d với một đường thẳng d’ nằm trong mặt phẳng (α).
Vấn đề 3. Chứng minh ba điểm thẳng hàng: Để chứng ba điểm thẳng hàng, ta có thể chứng minh chúng cùng thuộc hai mặt phẳng riêng biệt.
§2. HAI ĐƯỜNG THẲNG CHÉO NHAU VÀ HAI ĐƯỜNG THẲNG SONG SONG
Vấn đề 1. Tìm giao tuyến hai mặt phẳng: Nếu hai mặt phẳng (α) và (β) có điểm chung là S và lần lượt chứa hai đường thẳng song song d và d’ thì giao tuyến của (α) và (β) là đường thẳng ∆ qua S và song song với d và d’.
[ads]
Vấn đề 2. Tìm thiết điện của hình chóp khi cắt bởi một mặt phẳng: Ta tìm giao tuyến của mặt phẳng đó với các mặt bên của hình chóp. Đoạn nối giữa các giao tuyến cho ta một hình. Hình đó là thiết diện cần tìm.
Vấn đề 3. Chứng minh hai đường thẳng song song:
+ Chứng minh chúng cùng thuộc một mặt phẳng và dùng phương pháp chứng minh hai đường thẳng song song trong hình học phẳng (như tính chất đường trung bình của tam giác, định lí Talét đảo, tính chất song song của hai đường thẳng cùng vuông góc với đường thẳng thứ ba, …).
+ Chứng minh chúng cùng song song với đường thẳng thứ ba.
+ Dùng tính chất: Hai mặt phẳng phân biệt lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng(nếu có) cũng song song với hai đường thẳng ấy.
+ Dùng định lý về giao tuyến của ba mặt phẳng.
§3. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG
Vấn đề 1. Chứng minh đường thẳng song song với mặt phẳng: Để chứng minh đường thẳng d song song với mặt phẳng (α) ta chứng minh d không nằm trong (α) và song song với đường thẳng a chứa trong (α).
Vấn đề 2. Dựng thiết diện song song với một đường thẳng:
+ Cho đường thẳng d song song với mặt phẳng (α). Nếu mặt phẳng (β) chứa d và cắt (α) theo giao tuyến d’ thì d’ song song với d.
+ Thiết diện cắt bởi một mặt phẳng chứa một đường thẳng song song với một đường thẳng cho trước được xác định bằng cách phối hợp hai cách xác định giao tuyến đã biết.
§4. HAI MẶT PHẲNG SONG SONG
Vấn đề. Chứng minh hai mặt phẳng song song:
+ Vận dụng định lí Nếu mặt phẳng (α) chứa hai đường thẳng cắt nhau a, b và a, b cùng song với mặt phẳng (β) thì (α) song song với (β).
+ Ta chứng minh hai mặt phẳng (α) và (β) cùng song song với mặt phẳng thứ ba (γ).
§5. PHÉP CHIẾU SONG SONG
TỔNG HỢP CÁC DẠNG TOÁN CƠ BẢN CỦA HÌNH HỌC 11 CHƯƠNG 2
TRẮC NGHIỆM ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN – QUAN HỆ SONG SONG
MỘT SỐ ĐỀ ÔN KIỂM TRA MỘT TIẾT HÌNH HỌC 11 CHƯƠNG 2