Với mục đích kiểm tra đánh giá chủ đề kiến thức ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số sau khi học sinh đã được học xong, trường THPT Nguyễn Bỉnh Khiêm – Chư Sê – Gia Lai tổ chức kiểm tra tập trung Giải tích 12 chương 1 năm học 2019 – 2020.
Đề kiểm tra chương 1 Giải tích 12 năm học 2019 – 2020 trường THPT Nguyễn Bỉnh Khiêm – Gia Lai có mã đề 155, đề gồm 25 câu hỏi và bài toán dạng trắc nghiệm khách quan, thời gian làm bài 45 phút, đề kiểm tra có đáp án mã đề 155.
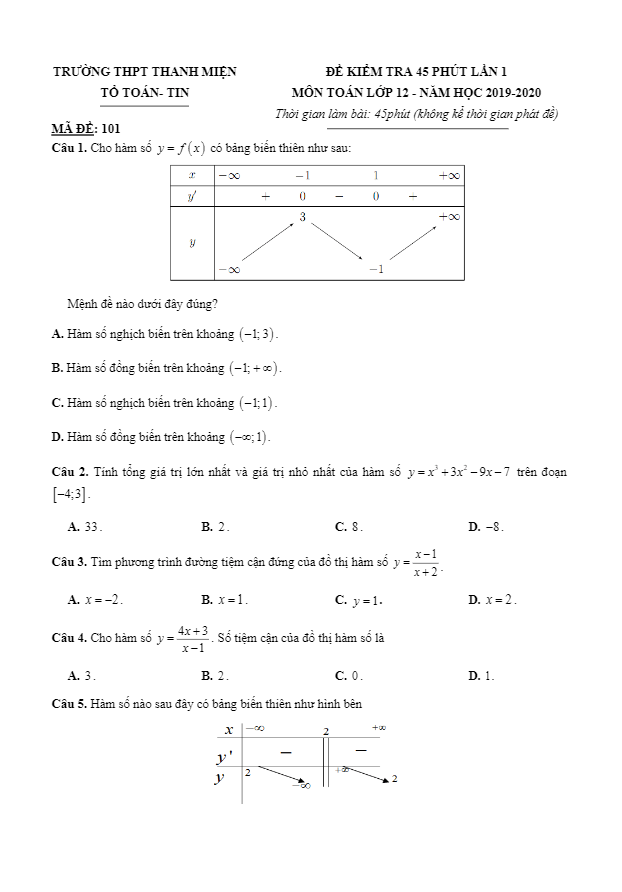
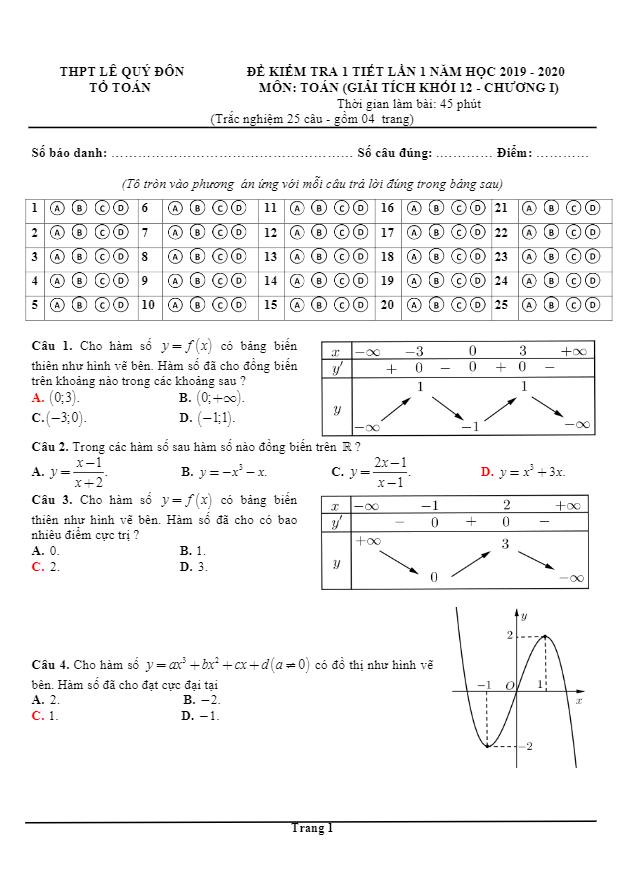
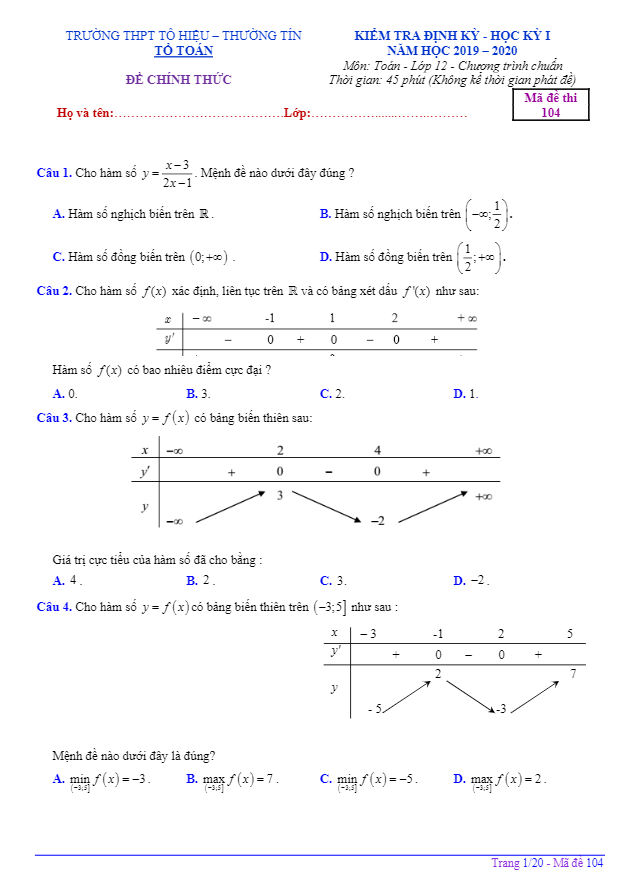
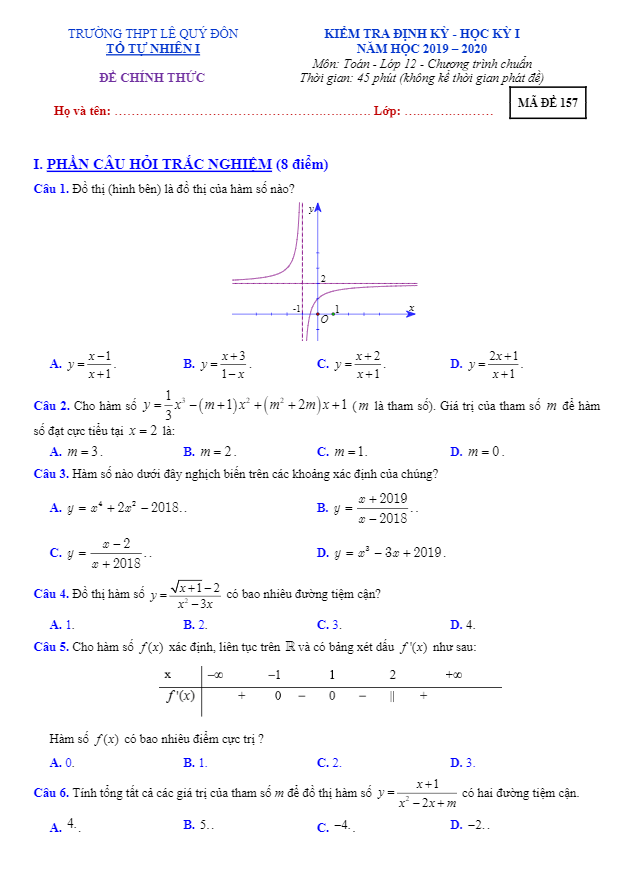
Trích dẫn đề kiểm tra chương 1 Giải tích 12 năm 2019 – 2020 trường Nguyễn Bỉnh Khiêm – Gia Lai:
+ Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để đường thẳng d: y = -x + m cắt đồ thị (C) của hàm số y = (-2x + 1)/(x + 1) tại hai điểm phân biệt A, B sao cho AB ≤ 2√2. Tổng tất cả các phần tử của S bằng?
[ads]
+ Cho hàm số y = f(x) có đồ thị (C) và lim f(x) = 2 khi x → -∞, lim f(x) = -2 khi x → +∞. Mệnh đề nào sau đây đúng?
A. (C) có đúng một tiệm cận ngang.
B. (C) có hai tiệm cận ngang là các đường thẳng x = 2 và x = -2.
C. (C) có hai tiệm cận ngang là các đường thẳng y = 2 và y = -2.
D. (C) không có tiệm cận ngang.
+ Cho hàm số y = (x + 3)/(x^2 – 6x + m). Có tất cả bao nhiêu giá trị thực của tham số m để đồ thị hàm số chỉ có một tiệm cận đứng và một tiệm cận ngang?
File WORD (dành cho quý thầy, cô): TẢI XUỐNG