Các bài toán tổ hợp là một phần quan trọng của chuyên ngành toán rời rạc và là một mảng khó trong chương trình toán THPT chuyên. Trong các kì thi học sinh giỏi quốc gia, Olympic Toán quốc tế và khu vực, những bài toán tổ hợp thường xuyên được đề cập và thường là những bài toán khó, mang tính chất phân loại. Đề thi VMO cũng như các đề thi Olympic 30/4, Olympic DHBB trong vài năm gần đây cũng đang có xu hướng giảm số lượng các bài toán hình học phẳng và thay vào đó là các bài toán tổ hợp. Tuy nhiên, so với các phân môn khác thì các bài toán tổ hợp đem lại không ít khó khăn rắc rối cho các em học sinh bậc Trung học phổ thông trong quá trình học cũng như trong các kỳ thi. Những học sinh mới bắt đầu làm quen một số dạng toán tổ hợp thường chưa hiểu tường tận tư tưởng cũng như phương pháp tiếp cận bài toán.
Để hiểu và vận dụng tốt một số dạng toán cơ bản và vận dụng kiến thức tổ hợp vào giải toán đòi hỏi học sinh phải có kiến thức nền tảng tổ hợp tương đối đầy đủ và chắc chắn trên tất cả các lĩnh vực của ngành toán rời rạc. Đó là một khó khăn rất lớn đối với giáo viên và học sinh khi giảng dạy và học tập phần này. Chính vì khó nên dẫn đến nhiều học sinh nản trong quá trình học, có tâm lý sợ các bài toán tổ hợp và có xu hướng không đầu tư cho việc giải chúng trong các kỳ thi mà để dành thời gian cho các bài toán thuộc các phân môn khác. Từ đó có thể thấy khó khăn lớn nhất của giáo viên là làm sao để học sinh hứng thú học và có khả năng vận dụng các phương pháp vào giải các bài toán tổ hợp, do đó vấn đề đặt ra là cần trang bị cho các em những kiến thức gì? Cần bắt đầu từ những bài toán nào? Cần phân dạng các bài tập áp dụng từng phương pháp giải toán tổ hợp theo mức độ từ thấp đến cao và những dấu hiệu của các bài toán như thế nào thì dùng phương pháp tương ứng?

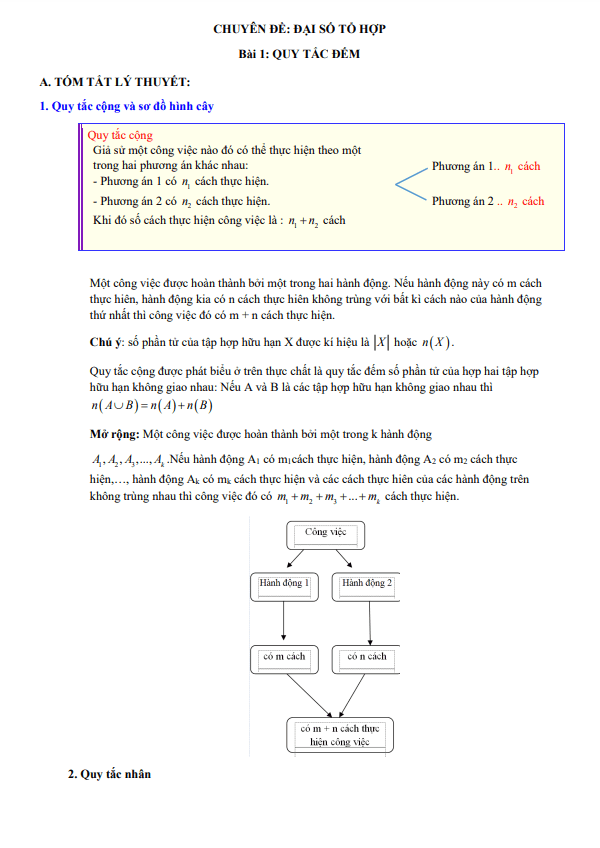
Một trong những vấn đề đầu tiên của tổ hợp là đếm xem có bao nhiêu phần tử của một tập hợp, bao nhiêu cách để giải quyết một công việc, bao nhiêu cấu hình được tạo ra với các quy tắc cho trước. Để đếm được chính xác, chúng ta phải phân biệt được các cấu hình dựa vào các quy luật xây dựng chúng. Vì thế, có thể xem bài toán đếm là những bài toán luyện tập đầu tiên để chúng ta làm quen với tư duy tổ hợp, điều này giải thích vì sao một số bài toán đếm đã được đưa vào phổ thông từ những năm mới đi học. Bài toán đếm rất phong phú kể cả dạng phát biểu đến cách giải. Độ khó của bài toán đếm được trải rất rộng: từ những bài toán dễ với các số liệu cụ thể, có thể kiểm chứng bằng trực giác đến những bài toán khó hơn, với những dữ liệu đầu vào bằng chữ mà kết quả của nó được biểu diễn bằng một công thức toán học. Có những công thức được tìm ra qua một vài suy luận đơn giản nhưng cũng có những công thức mà việc tìm thấy chúng phải kéo dài hàng thế kỷ. Có những bài toán đếm gặp rất nhiều khó khăn, bế tắc nếu như giải bằng phương pháp trực tiếp, trong khi giải bằng phương pháp gián tiếp lại trở nên rõ ràng, đơn giản.
Tuy nhiên, nói gì đi nữa thì tổ hợp vẫn là bài toán khó đối với học sinh và cả giáo viên. Toán tổ hợp cũng có nhiều dạng khiến người mới tiếp cận không khỏi lúng túng không biết bắt đầu từ đâu. Với tất cả những khó khăn và thuận lợi trên chúng tôi chọn đề tài “Một số phương pháp đếm trong các bài toán tổ hợp” để trao đổi với quý thầy cô và các em học sinh. Chuyên đề không có tham vọng đưa ra những vấn đề “thời sự”, những khám phá mới mẻ mà chúng tôi cố gắng trình bày lại các phương pháp đếm thường hay sử dụng như phương pháp đếm bằng xây dựng mô hình, đếm bằng hai cách, đếm bằng quan hệ truy hồi, đếm bằng ánh xạ, đếm bằng số phức thông qua hệ thống bài tập được chọn lọc từ cơ bản đến những bài toán trong các kỳ thi học sinh giỏi Quốc gia, Olympic toán Quốc tế và khu vực, Olympic toán của các nước . . . với hy vọng giúp các em học sinh có được các cách tiếp cận một cách có hệ thống với những bài toán tổ hợp “khó mà cực kỳ hấp dẫn” này.