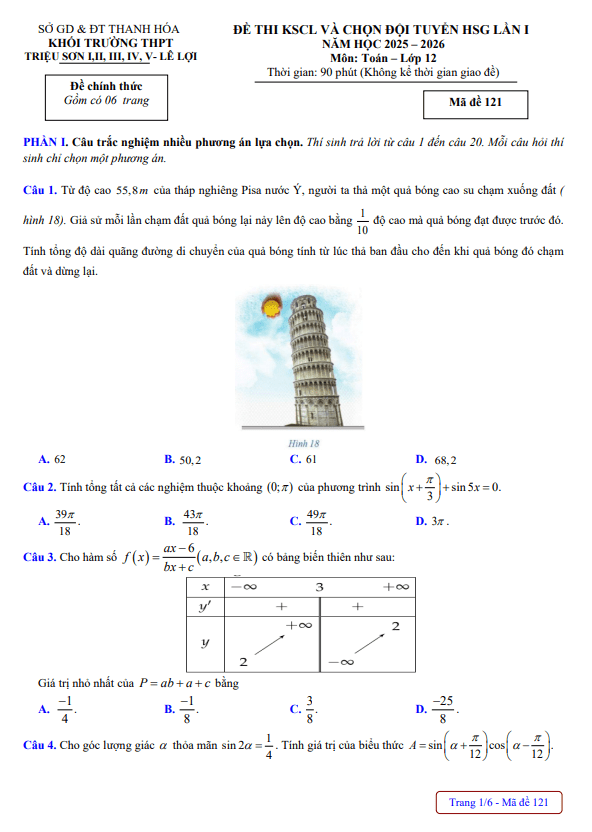
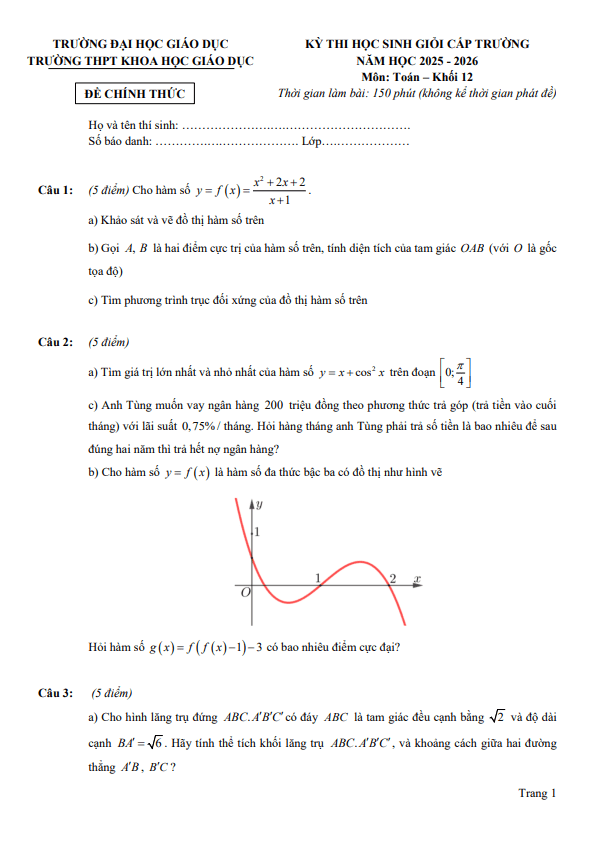
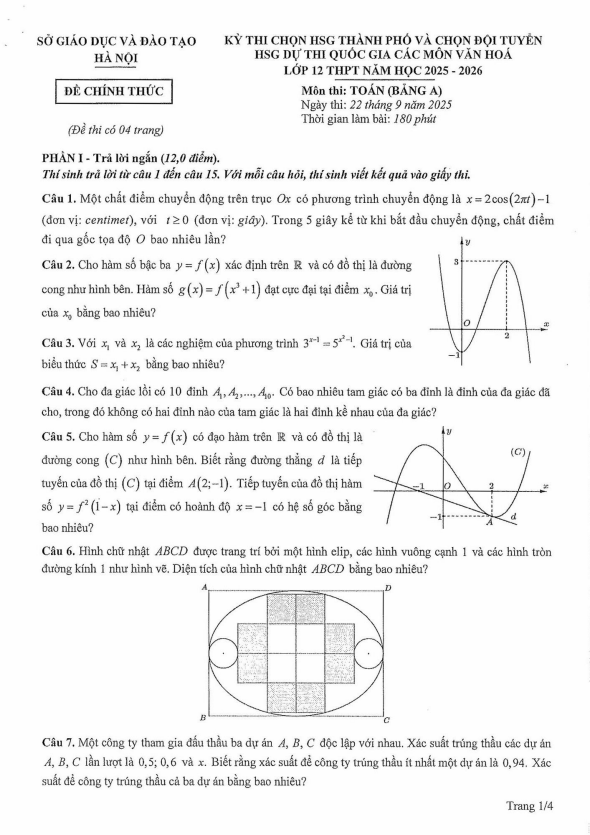
Đề thi chọn đội tuyển tham dự kỳ thi HSG Quốc gia Toán 12 năm 2019 sở GD và ĐT Lạng Sơn gồm 1 trang với 5 bài toán tự luận, thí sinh làm bài trong thời gian 180 phút (không kể thời gian giao đề), kỳ thi được tổ chức ngày 24 tháng 08 năm 2018, đề thi có lời giải chi tiết.
Trích dẫn đề thi chọn đội tuyển tham dự kỳ thi HSG Quốc gia Toán 12 năm 2019 sở GD và ĐT Lạng Sơn:
+ Trên mặt phẳng cho 2n^2 (n ≥ 2) đường thẳng sao cho không có hai đường nào song song và không có ba đường nào đồng quy. Các đường thẳng này chia mặt phẳng ra thành các miền rời nhau. Trong các miền đó, gọi F là tập tất cả các miền đa giác có diện tích hữu hạn. Chứng minh rằng có thể tô n đường thẳng trong số 2n^2 đường thẳng đã cho bằng màu xanh sao cho không có miền nào trong tập F có tất cả các cạnh màu xanh.
[ads]
+ Cho hình chữ nhật ABCD nội tiếp đường tròn (O). Gọi M, N lần lượt là trung điểm các cung nhỏ BC, AD. Gọi I, J lần lượt là trung điểm của OM, ON. Gọi K là điểm đối xứng với O qua M. Chứng minh rằng tứ giác BJDK nội tiếp đường tròn. Gọi P, Q lần lượt là hình chiếu vuông góc của I lên AB, AC. Chứng minh rằng AK ⊥ PQ.
+ Cho đa thức P(x) có hệ số nguyên, bậc 2 và hệ số bậc 2 bằng 1 thỏa mãn tồn tại đa thức Q(x) có hệ số nguyên sao cho P(x).Q(x) là đa thức có tất cả các hệ số đều là ±1. Chứng minh rằng nếu đa thức P(x) có nghiệm thực x0 thì |x0| < 2. Tìm tất cả các đa thức P(x).