Bài viết hướng dẫn phương pháp giải các dạng toán giá trị lớn nhất, giá trị nhỏ nhất của hàm số (GTLN – GTNN của hàm số) trong chương trình Giải tích 12 chương 1.
A. TÓM TẮT SÁCH GIÁO KHOA
Giả sử hàm số $f$ xác định trên tập hợp $X \subset R.$
a) Nếu tồn tại một điểm ${x_0} \in X$ sao cho $f(x) \le f\left( {{x_0}} \right)$ với mọi $x \in X$ thì số $M = f\left( {{x_0}} \right)$ được gọi là giá trị lớn nhất của hàm số $f$ trên $X.$
Kí hiệu: $M = \mathop {\max }\limits_{x \in X} f(x).$
b) Nếu tồn tại một điểm ${x_0} \in X$ sao cho $f(x) \ge f\left( {{x_0}} \right)$ với mọi $x \in X$ thì số $m = f\left( {{x_0}} \right)$ được gọi là giá trị nhỏ nhất của hàm số $f$ trên $X.$
Kí hiệu: $m = \mathop {\min }\limits_{x \in X} f(x).$
B. PHƯƠNG PHÁP GIẢI TOÁN
Tùy theo tập hợp $X$ và hàm số $f$ ta có thể sử dụng một trong các phương pháp sau:
Vấn đề 1: Tìm giá trị lớn nhất, nhỏ nhất của hàm số $f(x)$ trên $X = [a; b].$
1. PHƯƠNG PHÁP:
Nếu hàm số $f(x)$ liên tục trên đoạn $[a;b]$ và $f(x)$ có đạo hàm trên $(a;b)$, có thể tìm GTLN và GTNN của hàm số $f(x)$ trên đoạn $[a;b]$ theo quy tắc sau:
Bước 1. Tìm các điểm ${x_i} \in (a;b)$ $(i = 1,2, \ldots )$ mà tại các điểm đó hàm số $f(x)$ có đạo hàm bằng $0.$
Bước 2. Tính các giá trị $f\left( {{x_i}} \right)$ $(i = 1,2, \ldots )$, $f(a)$ và $f(b).$
Bước 3. Số lớn nhất trong các giá trị trên là GTLN của hàm số $f(x)$ trên đoạn $[a;b].$ Số nhỏ nhất trong các giá trị trên là GTNN của hàm số $f(x)$ trên đoạn $[a;b].$
Chú ý: Khi bài toán không chỉ rõ tập hợp $X$ thì ta hiểu tập $X$ chính là tập xác định $D$ của hàm số.
2. CÁC VÍ DỤ:
Ví dụ 1: Tìm GTLN và GTNN của hàm số: $f(x) = {x^3} – 3x + 2$ trên đoạn $[0;2].$
Tập xác định: $D = R$, $X = [0;2].$
$f'(x) = 3{x^2} – 3.$
$f'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 1 \in X}\\
{x = – 1 \notin X}
\end{array}} \right..$
Ta có: $f(0) = 2$, $f(1) = 0$ và $f(2) = 4.$
Vì $f$ là hàm số liên tục trên $[0; 2]$ nên ta có:
$\mathop {\max }\limits_{x \in [0;2]} f(x) = 4$ đạt tại $x = 2.$
$\mathop {\min }\limits_{x \in [0;2]} f(x) = 0$ đạt tại $x = 1.$
Ví dụ 2: Tìm GTLN và GTNN của hàm số: $f(x) = \sqrt {x – 1} + \sqrt {9 – x} .$
Tập xác định: $D = [1;9]$, $X = D = [1;9].$
$f'(x) = \frac{1}{{2\sqrt {x – 1} }} – \frac{1}{{2\sqrt {9 – x} }}$ $ = \frac{{\sqrt {9 – x} – \sqrt {x – 1} }}{{2\sqrt {x – 1} .\sqrt {9 – x} }}.$
$f'(x) = 0$ $ \Leftrightarrow \sqrt {9 – x} = \sqrt {x – 1} $ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x – 1 \ge 0}\\
{9 – x = x – 1}
\end{array}} \right.$ $ \Leftrightarrow x = 5 \in X.$
Ta có: $f(1) = \sqrt 8 $, $f(5) = 4$ và $f(9) = \sqrt 8 .$
Vì $f$ là hàm số liên tục trên $[1;9]$ nên ta có:
$\mathop {\max }\limits_X f(x) = 4$ đạt tại $x = 5.$
$\mathop {\min }\limits_X f(x) = \sqrt 8 $ đạt tại $x = 1$ hay $x = 9.$
3. BÀI TẬP:
1. Tìm GTLN và GTNN của các hàm số:
a) $f(x) = \frac{{{x^3}}}{3} + 2{x^2} + 3x – 4$ trên $[ – 4;0].$
b) $f(x) = \frac{{2{x^2} + 5x + 4}}{{x + 2}}$ trên $[ – 1;1].$
c) $f(x) = \left| {{x^2} – 3x + 2} \right| – 3$ trên $[ – 10;10].$
d) $f(x) = x – \sin 2x$ trên $\left[ { – \frac{\pi }{2};\pi } \right].$
2. Tìm GTLN và GTNN của hàm số $y = 5\cos x – \cos 5x$ trên $\left[ { – \frac{\pi }{4}:\frac{\pi }{4}} \right].$
3. Tìm GTLN và GTNN của hàm số $y = \frac{{x + 1}}{{\sqrt {{x^2} + 1} }}$ trên $[ – 1;2].$
4. Tìm GTLN và GTNN của các hàm số:
a) $y = x + \sqrt {4 – {x^2}} .$
b) $y = x + \sqrt {12 – 3{x^2}} .$
c) $y = \sqrt {4 – {x^2}} (x + 2).$
d) $y = (3 – x)\sqrt {{x^2} + 1} $ với $x \in [0;2].$
5. Tìm GTLN và GTNN của hàm số: $y = {x^4} – 3{x^3} – 2{x^2} + 9x$ trên $[ – 2;2].$
Vấn đề 2: Tìm giá trị lớn nhất, nhỏ nhất của hàm số $f$ trên tập $X$ không là một đoạn.
1. PHƯƠNG PHÁP:
Phương pháp thường dùng để tìm GTLN và GTNN của hàm số trên một tập hợp $X \ne [a;b]$ ta thực hiện các bước sau:
+ Tìm tập xác định $D$ và tập $X.$
+ Tìm $y’$ và giải phương trình $y’ = 0.$
+ Tìm các giới hạn khi $x$ dần tới các điểm đầu khoảng của $X.$
+ Lập bảng biến thiên của hàm số trên tập hợp $X.$
+ Dựa vào bảng biến thiên suy ra GTLN hay GTNN của hàm số trên $X.$
2. CÁC VÍ DỤ:
Ví dụ 1: Tìm GTLN và GTNN của hàm số $f(x) = x + \frac{1}{{x – 1}}$ trên khoảng $(1; + \infty ).$
Tập xác định: $D = R\backslash \{ 1\} $, $X = (1; + \infty ).$
$y’ = 1 – \frac{1}{{{{(x – 1)}^2}}} = \frac{{{x^2} – 2x}}{{{{(x – 1)}^2}}}.$
$y’ = 0$ $ \Leftrightarrow x = 0$ hay $x = 2.$
$\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty $, $\mathop {\lim }\limits_{x \to {1^ + }} f(x) = + \infty .$
Bảng biến thiên:

Dựa vào bảng biến thiên ta suy ra: $\mathop {\min }\limits_X f(x) = 3$ đạt tại $x = 2.$ Hàm số không đạt giá trị lớn nhất trên $X.$
3. BÀI TẬP:
1. Tìm GTLN và GTNN của các hàm số:
a) $f(x) = \frac{{15\left( {{x^2} + 1} \right)}}{{2{x^2} + x + 2}}.$
b) $y = \frac{{21\left( {{x^2} + 3} \right)}}{{{x^2} + x + 2}}.$
2. Tìm giá trị lớn nhất và nhỏ nhất của hàm số $y = x + \sqrt {2{x^2} + 1} .$
Vấn đề 3: Tìm giá trị lớn nhất, nhỏ nhất của hàm số $f$ trên $X$ bằng cách dùng ẩn phụ.
1. PHƯƠNG PHÁP:
Một số hàm số là hàm số phụ thuộc biểu thức $k(x)$, ta có thể đổi biển số và thực hiện các bước sau:
Bước 1: Đặt $t = k(x).$
Bước 2: Xác định điều kiện của $t$ bằng cách tìm tập giá trị của hàm số $t = k(x)$ trên $X.$ Giả sử ta được: $x \in X \Leftrightarrow t \in T.$
Bước 3: Đưa hàm số $f(x)$ về dạng hàm số của đối số ta được $f(x) = g(t).$
Bước 4: Tìm GTLN, GTNN của $g(t)$ trên $T.$
Kết luận: $\mathop {\max }\limits_{x \in X} f(x) = \mathop {\max }\limits_{t \in T} g(t)$ và $\mathop {\min }\limits_{x \in X} f(x) = \mathop {\min }\limits_{t \in T} g(t).$
2. CÁC VÍ DỤ:
Ví dụ 1: Tìm GTLN và GTNN của hàm số $f(x) = \cos 2x + 2\sin x – 3$ trên $\left[ { – \frac{\pi }{6};\frac{{5\pi }}{6}} \right].$
Đặt $t = \sin x.$
Ta có: $x \in X = \left[ { – \frac{\pi }{6};\frac{{5\pi }}{6}} \right]$ $ \Leftrightarrow t \in \left[ { – \frac{1}{2};1} \right] = T.$
Khi đó: $f(x) = – 2{\sin ^2}x + 2\sin x – 2$ $ = – 2{t^2} + 2t – 2 = g(t).$
Ta có: $g'(t) = – 4t + 2.$
$g'(t) = 0$ $ \Leftrightarrow t = \frac{1}{2} \in \left[ { – \frac{1}{2};1} \right].$
$g\left( { – \frac{1}{2}} \right) = – \frac{7}{2}$, $g\left( {\frac{1}{2}} \right) = – \frac{3}{2}$ và $g(1) = – 2.$
Vậy:
$\mathop {\max }\limits_X f(x) = \mathop {\max }\limits_T g(t) = g\left( {\frac{1}{2}} \right) = – \frac{3}{2}.$
$\mathop {\min }\limits_X f(x) = \mathop {\min }\limits_T g(t) = g\left( { – \frac{1}{2}} \right) = – \frac{7}{2}.$
Ví dụ 2: Tìm GTLN và GTNN của hàm số $f(x) = \sqrt {5 – x} + \sqrt {x – 1} – \sqrt {(x – 1)(5 – x)} + 5.$
Tập xác định: $D = [1;5]$, $X = D.$
Đặt $t = \sqrt {5 – x} + \sqrt {x – 1} .$
Ta có: $t’ = \frac{{ – 1}}{{2\sqrt {5 – x} }} + \frac{1}{{2\sqrt {x – 1} }}$ $ = \frac{{\sqrt {5 – x} – \sqrt {x – 1} }}{{2\sqrt {x – 1} .\sqrt {5 – x} }}.$
$t’ = 0 \Leftrightarrow x = 3.$
$t(1) = 2$, $t(3) = 2\sqrt 2 $ và $t(5) = 2.$
Vậy $\mathop {\max }\limits_{[1;5]} t = 2\sqrt 2 $, $\mathop {\min }\limits_{[1;5]} t = 2.$
Do đó: $x \in [1;5]$ $ \Leftrightarrow t \in T = [2;2\sqrt 2 ].$
Khi đó ${t^2} = 4 + 2\sqrt {(5 – x)(x – 1)} $ $ \Rightarrow \sqrt {(5 – x)(x – 1)} = \frac{{{t^2} – 4}}{2}.$
Do đó: $f(x) = t – \frac{{{t^2} – 4}}{2} + 5$ $ = – \frac{1}{2}{t^2} + t + 7 = g(t).$
Ta có: $g'(t) = – t + 1$, $g'(t) = 0$ $ \Leftrightarrow t = 1 \in [2;2\sqrt 2 ].$
$g(2) = 7$, $g(1) = \frac{{15}}{2}$ và $g(2\sqrt 2 ) = 3 + 2\sqrt 2 .$
Vậy:
$\mathop {\max }\limits_X f(x) = \mathop {\max }\limits_T g(t) = g(1) = \frac{{15}}{2}.$
$\mathop {\min }\limits_X f(x) = \mathop {\min }\limits_T g(t) = g(2\sqrt 2 ) = 3 + 2\sqrt 2 .$
3. BÀI TẬP:
1. Tìm GTLN và GTNN của các hàm số:
a) $f(x) = {\cos ^2}2x – 2\sqrt 3 \sin x.\cos x + 6.$
b) $f(x) = {\sin ^4}x + {\cos ^2}x + 2.$
c) $f(x) = \frac{{9{{\sin }^2}x – \sin x + 1}}{{9{{\sin }^2}x + \sin x + 1}}$ trên $\left[ {0;\frac{\pi }{6}} \right].$
d) $f(x) = {\left( {\frac{{{x^2} + x + 1}}{{{x^2} – x + 1}}} \right)^3}$ $ – 3{\left( {\frac{{{x^2} + x + 1}}{{{x^2} – x + 1}}} \right)^2} + 10.$
e) $y = \frac{{\sin x + 1}}{{{{\sin }^2}x + \sin x + 1}}.$
2. Tìm GTLN và GTNN của các hàm số:
a) $y = \frac{{{{\sin }^4}x + {{\cos }^4}x}}{{{{\sin }^6}x + {{\cos }^6}x}}.$
b) $y = 2(1 + \sin 2x\cos 4x)$ $ – \frac{1}{2}(\cos 4x – \cos 8x).$
Vấn đề 4: Giá trị lớn nhất – nhỏ nhất và điều kiện của tham số thỏa mãn điều kiện về nghiệm của phương trình, bất phương trình.
1. PHƯƠNG PHÁP:
a) Để xác định số nghiệm của phương trình $f(x) = m$ $(1)$ trên tập hợp $X$ ta làm như sau:
+ Lập bảng biến thiên của hàm số $f(x)$ trên tập hợp $X.$
+ Dựa vào bảng biến thiên ta xác định được số giao điểm của đồ thị $(C): y = f(x)$ với đồ thị $(d): y = m.$
+ Từ đó suy ra số nghiệm của phương trình trên tập $X.$
$(1)$ có nghiệm $x \in X$ $ \Leftrightarrow (d)$ và phần đồ thị $(C)$ trên $X$ có giao điểm.
$(1)$ có $k$ nghiệm $x \in X$ $ \Leftrightarrow (d)$ và phần đồ thị $(C)$ trên $X$ có $k$ giao điểm.
b) Giả sử trên $X$ hàm số đạt giá trị nhỏ nhất và giá trị lớn nhất.
Khi đó:
Bất phương trình $f(x) \le m$ có nghiệm $x \in X$ $ \Leftrightarrow \mathop {\min }\limits_{x \in X} f(x) \le m.$
Bất phương trình $f(x) \le m$ thỏa mãn với mọi $x \in X$ $ \Leftrightarrow \mathop {\max }\limits_{x \in X} f(x) \le m.$
Bất phương trình $f(x) < m$ có nghiệm $x \in X$ $ \Leftrightarrow \mathop {\min }\limits_{x \in X} f(x) < m.$
Bất phương trình $f(x) < m$ thỏa mãn với mọi $x \in X$ $ \Leftrightarrow \mathop {\max }\limits_{x \in X} f(x) < m.$
2. CÁC VÍ DỤ:
Ví dụ 1: Tìm tham số $m$ để phương trình ${x^3} – 6{x^2} + m = 0$ $(*)$ có ba nghiệm phân biệt.
Ta có: $(*) \Leftrightarrow m = – {x^3} + 6{x^2}.$
Do đó $(*)$ là phương trình hoành độ giao điểm của $(d):y = m$ và $(C):y = – {x^3} + 6{x^2}.$
Xét hàm số $y = – {x^3} + 6{x^2}$:
Tập xác định: $D = R.$
$y’ = – 3{x^2} + 12x$, $y’ = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0 \Rightarrow y = 0}\\
{x = 4 \Rightarrow y = 32}
\end{array}} \right..$
Bảng biến thiên:

Dựa vào bảng biến thiên ta có:
$(*)$ có nghiệm ba nghiệm phân biệt thuộc $[-1;6]$ $ \Leftrightarrow (d)$ và phần đồ thị $(C)$ với $x \in [ – 1;6]$ có ba giao điểm phân biệt $ \Leftrightarrow 0 < m \le 7.$
Ví dụ 2: Tìm tham số $m$ để phương trình $x\sqrt x + \sqrt {x + 16} = m(\sqrt {25 – x} + \sqrt {9 – x} )$ $(1)$ có nghiệm.
Điều kiện: $0 \le x \le 9.$
Khi đó: $(1) \Leftrightarrow m = \frac{{x\sqrt x + \sqrt {x + 16} }}{{\sqrt {25 – x} + \sqrt {9 – x} }} = F(x).$
Ta có: $f(x) = x\sqrt x + \sqrt {x + 16} $ có $f'(x) = \frac{{3\sqrt x }}{2} + \frac{1}{{2\sqrt {x + 16} }} > 0$, $\forall x \in [0;9].$
$ \Rightarrow f(x)$ tăng trên $[0;9]$ và $f(x) > 0$, $\forall x \in [0;9].$
$g(x) = \sqrt {25 – x} + \sqrt {9 – x} $ có $g'(x) = \frac{{ – 1}}{{2\sqrt {25 – x} }} + \frac{{ – 1}}{{2\sqrt {9 – x} }} < 0$, $\forall x \in [0;9].$
$ \Rightarrow g(x)$ giảm trên $[0;9]$ và $g(x) > 0$, $\forall x \in [0;9].$
Do đó $F(x)$ là hàm số tăng trên $[0;9].$
Ta có bảng biến thiên:

Do đó $(1)$ có nghiệm $ \Leftrightarrow \frac{1}{2} \le m \le 8.$
Ví dụ 3: Tìm $m$ để bất phương trình $x + \sqrt {2{x^2} + 2} > m$ $(1)$ có tập nghiệm là $R.$
Xét hàm số $f(x) = x + \sqrt {2{x^2} + 2} .$
Tập xác định: $D = R.$
$f'(x) = 1 + \frac{{4x}}{{2\sqrt {2{x^2} + 2} }}$ $ = \frac{{\sqrt {2{x^2} + 2} + 2x}}{{\sqrt {2{x^2} + 2} }}.$
$f'(x) = 0 \Leftrightarrow \sqrt {2{x^2} + 2} = – 2x$ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x \le 0}\\
{2{x^2} + 2 = 4{x^2}}
\end{array}} \right.$ $ \Leftrightarrow x = – 1.$
$\mathop {\lim }\limits_{x \to + \infty } f(x)$ $ = \mathop {\lim }\limits_{x \to + \infty } x\left( {1 + \sqrt {2 + \frac{2}{{{x^2}}}} } \right) = + \infty .$
$\mathop {\lim }\limits_{x \to – \infty } f(x)$ $ = \mathop {\lim }\limits_{x \to – \infty } x\left( {1 – \sqrt {2 + \frac{2}{{{x^2}}}} } \right) = + \infty .$
Bảng biến thiên:

Dựa vào bảng biến thiên ta có: $(1)$ có tập nghiệm là $R$ $ \Leftrightarrow m < 1.$
Ví dụ 4: Tìm $m$ để bất phương trình $\sqrt {4x – 8} + \sqrt {16 – 4x} \le m$ $(1)$ có nghiệm.
Xét hàm số $f(x) = \sqrt {4x – 8} + \sqrt {16 – 4x} .$
Tập xác định: $D = [2;4].$
$f'(x) = \frac{4}{{2\sqrt {4x – 8} }} + \frac{{ – 4}}{{2\sqrt {16 – 4x} }}$ $ = 2.\frac{{\sqrt {16 – 4x} – \sqrt {4x – 8} }}{{\sqrt {16 – 4x} .\sqrt {4x – 8} }}.$
$f'(x) = 0$ $ \Leftrightarrow \sqrt {16 – 4x} = \sqrt {4x – 8} $ $ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{\frac{1}{2} \le x \le 4}\\
{16 – 4x = 4x – 8}
\end{array}} \right.$ $ \Leftrightarrow x = 3.$
Bảng biến thiên:
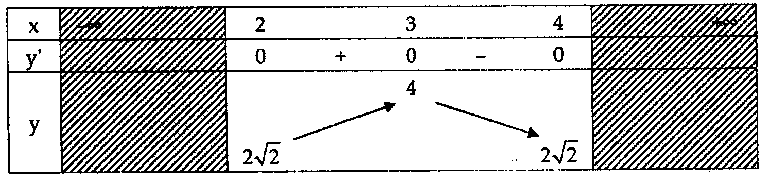
Dựa vào bảng biến thiên ta có: $(1)$ có nghiệm $ \Leftrightarrow m \ge 2\sqrt 2 .$
3. BÀI TẬP:
I. Phương trình:
1. Cho phương trình ${\sin ^6}x + {\cos ^6}x = m\sin 2x.$ Với giá trị nào của tham số $m$ thì phương trình có nghiệm.
2. Tìm tham số $m$ để phương trình $\sqrt {1 + x} + \sqrt {3 – x} – \sqrt {(1 + x)(3 – x)} = m$ có nghiệm.
3. Cho phương trình $\sin 2x + 2\sin x = m.$ Tìm $m$ để phương trình có đúng hai nghiệm thuộc đoạn $\left[ {0;\frac{{5\pi }}{4}} \right].$
4. Tìm $m$ để phương trình $\frac{{4\sin x + 2}}{{\sin x + 2}} = m$ có đúng hai nghiệm thuộc đoạn $[0;\pi ].$
5. Cho phương trình $4\cos x.\cos 2x.\cos 3x + m$ $ = 14\left( {{{\cos }^2}x – {{\sin }^2}x} \right).$ Với giá trị nào của tham số $m$ thì phương trình có nghiệm thuộc đoạn $\left[ { – \frac{\pi }{3}; – \frac{\pi }{6}} \right].$
II. Bất phương trình:
1. Tìm $m$ để bất phương trình $m\sqrt {2{x^2} + 9} < x + m$ có nghiệm.
2. Tìm $m$ để bất phương trình $\sqrt {(1 + x)(3 – x)} \ge m + \left( {{x^2} – 2x – 3} \right)$ nghiệm đúng $\forall x \in [ – 1;3].$
3. Cho bất phương trình $x + 2m \le \sqrt {4x – {x^2}} .$ Tìm $m$ để bất phương trình có nghiệm.
4. Định $m$ để bất phương trình $mx + 2 \ge \sqrt {4x – {x^2}} $ thỏa mãn với mọi $x \in (0;4].$









