Bài viết hướng dẫn phương pháp giải bài toán xét tính đơn điệu của hàm số dựa vào bảng biến thiên, đồ thị của hàm số.
1. Bài tập minh họa
Bài 1. Cho hàm số $y = f(x)$ có bảng biến thiên sau:

Hàm số $y = f(x)$ đồng biến trên khoảng nào sau đây?
A. $( – \infty ;5).$
B. $(0;2).$
C. $(2; + \infty ).$
D. $(0; + \infty ).$
Dựa vào bảng biến thiên, ta thấy đồ thị của hàm số $y = f(x)$ là đường đi lên theo chiều từ trái sang phải trên khoảng $(2; + \infty ).$
Chọn đáp án C.
Bài 2. Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
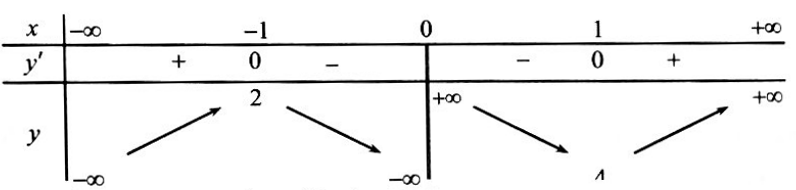
Hàm số nghịch biến trong khoảng nào?
A. $( – 1;1).$
B. $(0;1).$
C. $(4; + \infty ).$
D. $( – \infty ;2).$
Dựa vào BBT ta có hàm số $y = f(x)$ nghịch biến trong khoảng $(0;1).$
Chọn đáp án B.
Bài 3. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ:
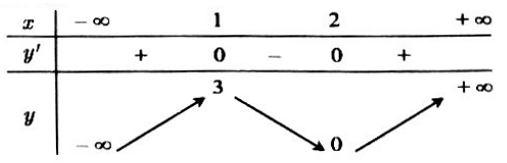
Mệnh đề nào sau đây là sai?
A. Hàm số đã cho đồng biến trên khoảng $( – \infty ;1).$
B. Hàm số đã cho nghịch biến trên khoảng $(0;3).$
C. Hàm số đã cho đồng biến trên khoảng $(2; + \infty ).$
D. Hàm số đã cho đồng biến trên khoảng $(3; + \infty ).$
Dựa vào bảng biến thiên ta thấy trên khoảng $(0;3)$ hàm số sẽ đồng biến trên khoảng $(0;1)$ và $(2;3).$
Chọn đáp án B.
Bài 4. Cho hàm số $y = f(x)$ có đồ thị hàm số như sau:

Mệnh đề nào dưới đây đúng?
A. Hàm số luôn đồng biến trên $R.$
B. Hàm số nghịch biến trên $(1; + \infty ).$
C. Hàm số đồng biến trên $( – 1; + \infty ).$
D. Hàm số nghịch biến trên $( – \infty ; – 1).$
Dựa vào đồ thị ta thấy hàm số nghịch biến trên $( – \infty ; – 1).$
Chọn đáp án D.
Bài 5. Cho hàm số $y = f(x).$ Đồ thị của hàm số $y = f'(x)$ như hình bên:
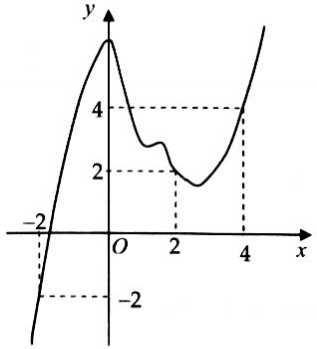
Đặt $h(x) = f(x) – \frac{{{x^2}}}{2}.$ Mệnh đề nào dưới đây đúng?
A. Hàm số $y = h(x)$ đồng biến trên khoảng $(-2;3).$
B. Hàm số $y = h(x)$ đồng biến trên khoảng $(0;4).$
C. Hàm số $y = h(x)$ nghịch biến trên khoảng $(0;1).$
D. Hàm số $y = h(x)$ nghịch biến trên khoảng $(2;4).$
Ta có $h'(x) = f'(x) – x.$

Từ đồ thị của $f'(x)$ và đường thẳng $y = x$ ta suy ra trên khoảng $(2;4)$ thì đồ thị $f'(x)$ nằm dưới đường thẳng $y = x.$ Do đó $h'(x) < 0$ trên $(2;4).$
Chọn đáp án D.
2. Bài tập tự luyện
Bài 1. Hàm số $y = f(x)$ có bảng biến thiên như sau:
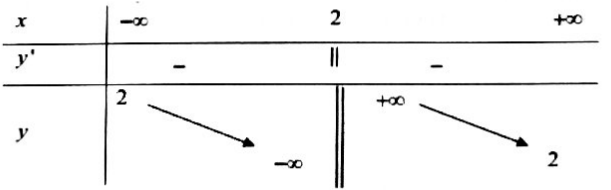
Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên $R\backslash \{ 2\} .$
B. Hàm số đồng biến trên $( – \infty ;2)$ và $(2; + \infty ).$
C. Hàm số nghịch biến trên $( – \infty ;2)$ và $(2; + \infty ).$
D. Hàm số nghịch biến trên $R.$
Bài 2. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ bên. Khẳng định nào sau đây là đúng?
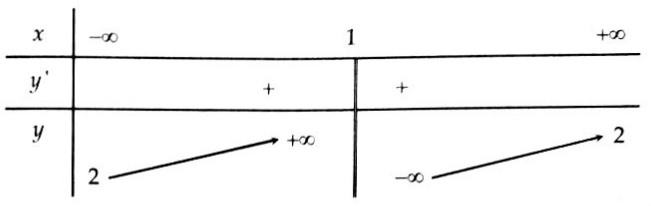
A. Hàm số $f(x)$ đồng biến trên các khoảng $( – \infty ;2)$ và $(2; + \infty ).$
B. Hàm số $f(x)$ đồng biến trên các khoảng $( – \infty ;1) \cup (1; + \infty ).$
C. Hàm số $f(x)$ đồng biến trên $R.$
D. Hàm số $f(x)$ đồng biến trên các khoảng $( – \infty ;1)$ và $(1; + \infty ).$
Bài 3. Cho hàm số $y = f(x)$ có bảng biến thiên như hình dưới đây:
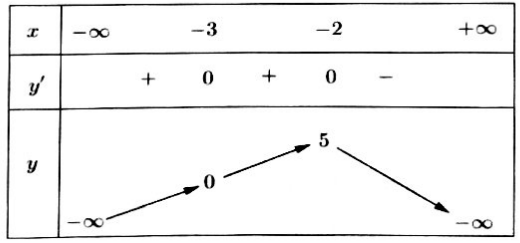
Số mệnh đề sai trong các mệnh đề sau đây?
I. Hàm số đồng biến trên khoảng $(-3;-2).$
II. Hàm số đồng biến trên khoảng $( – \infty ;5).$
III. Hàm số nghịch biến trên các khoảng $( – 2; + \infty ).$
IV. Hàm số đồng biến trên khoảng $( – \infty ; – 2).$
A. $2.$
B. $3.$
C. $4.$
D. $1.$
Bài 4. Cho hàm số $y = f(x)$ có bảng biến thiên như sau. Khẳng định nào dưới đây đúng?
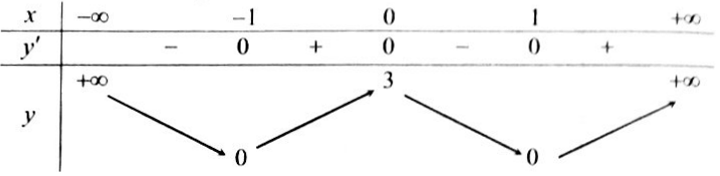
A. Hàm số đồng biến trên $(-1;1).$
B. Hàm số nghịch biến trên các khoảng $(-1;0)$ và $(1; + \infty ).$
C. Hàm số đồng biến trên các khoảng $(-1;0)$ và $(1; + \infty ).$
D. Hàm số đồng biến trên các khoảng $( – \infty ; – 1)$ và $(0;1).$
Bài 5. Cho hàm số $y = f(x)$ có bảng biến thiên như hình bên dưới. Mệnh đề nào sau đây đúng?
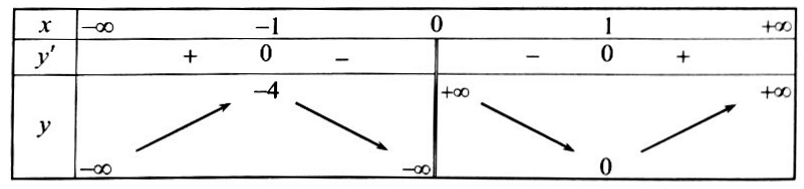
A. Hàm số đồng biến trên khoảng $(0; + \infty ).$
B. Hàm số nghịch biến trên khoảng $(-1;1).$
C. Hàm số đồng biến trên khoảng $(-1;0).$
D. Hàm số nghịch biến trên khoảng $(0;1).$
Bài 6. Cho hàm số $f(x) = \frac{{ax + b}}{{cx + d}}$ có đồ thị như hình bên dưới.

Xét các mệnh đề sau:
(I) Hàm số đồng biến trên các khoảng $( – \infty ;1)$ và $(1; + \infty ).$
(II) Hàm số nghịch biến trên các khoảng $( – \infty ; – 1)$ và $(1; + \infty ).$
(III) Hàm số đồng biến trên tập xác định.
Số các mệnh đề đúng là:
A. $2.$
B. $1.$
C. $0.$
D. $3.$
Bài 7. Cho hàm số $y = f(x)$ có đồ thị như hình vẽ bên dưới. Hàm số $y = f(x)$ nghịch biến trên khoảng nào dưới đây?
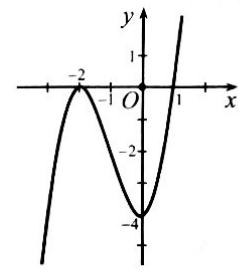
A. $( – 1;0).$
B. $(1; + \infty ).$
C. $( – \infty ; – 2).$
D. $( – 2;1).$
Bài 8. Cho hàm số $f(x)$ liên tục trên $R$ và có đồ thị như hình vẽ dưới đây, hàm số $f(x)$ đồng biến trên khoảng nào?

A. $( – \infty ;0)$.
B. $( – \infty ; – 1)$.
C. $(1; + \infty )$.
D. $( – 1;1).$
Bài 9. Cho hàm số $y = f(x)$ liên tục trên $R$ và có đồ thị như hình vẽ bên.
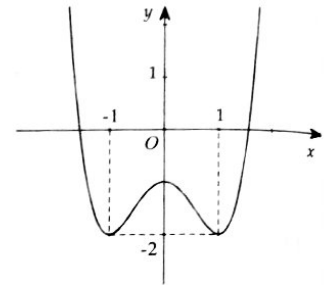
Hàm số $y = f(x)$ nghịch biến trên khoảng nào dưới đây?
A. $( – \infty ; – 1).$
B. $( – 1;1).$
C. $( – \infty ;0).$
D. $(0; + \infty ).$
Bài 10. Hàm số $y = f(x)$ có đồ thị như hình vẽ bên dưới.

Hàm số $y = -f(x)$ đồng biến trên khoảng:
A. $( – 2; + \infty ).$
B. $( – \infty ;1).$
C. $( – \infty ;0).$
D. $( – 1; + \infty ).$
ĐÁP ÁN BÀI TẬP TỰ LUYỆN
1. C.
2. D.
3. D.
4. C.
5. D.
6. B.
7. A.
8. C.
9. A.
10. D.









