Bài viết hướng dẫn giải các bài tập trong phần câu hỏi và bài tập và phần luyện tập của sách giáo khoa Hình học 12 cơ bản: Khái niệm về thể tích của khối đa diện.
CÂU HỎI VÀ BÀI TẬP
Bài 1. Tính thể tích khối tứ diện đều cạnh $a.$
Lời giải:

Gọi $BB’$, $CC’$ là các đường cao của tam giác $BCD.$ $O = BB’ \cap CC’$ ($O$ là tâm của tam giác đều $BCD$). Không khó khăn ta có thể chứng minh được $AO \bot (BCD)$ (chứng minh cho ${CD \bot \left( {ABB’} \right)}$, ${BD \bot \left( {ACC’} \right)}$).
Do vậy thể tích $V$ của khối chóp là:
$V = \frac{1}{3}AO.{S_{\Delta BCD}}$ $(1).$
Ta có: ${S_{\Delta BCD}} = \frac{1}{2}a.a.\sin {60^0} = \frac{{{a^2}\sqrt 3 }}{4}$ $(2).$
$AO = \sqrt {A{B^2} – B{O^2}} $ $ = \sqrt {A{B^2} – \frac{4}{9}BB{‘^2}} $ $ = \sqrt {{a^2} – \frac{4}{9}{{\left( {\frac{{a\sqrt 3 }}{2}} \right)}^2}} $ $ = a\sqrt {\frac{2}{3}} $ $(3).$
Thay $(2)$, $(3)$ vào $(1)$ ta có: $V = \frac{1}{3}.\frac{{a\sqrt 2 }}{{\sqrt 3 }}.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{\sqrt 2 {a^3}}}{{12}}.$
Bài 2. Tính thể tích khối bát diện đều cạnh $a.$
Lời giải:

Ta có: ${V_{ABCDEF}} = {V_{ABCDE}} + {V_{FBCDE}}.$
$ = 2{V_{ABCDE}} = 2.\frac{1}{3}{S_{OBCDE}}.AO$ ($O$ là tâm của hình vuông $BCDE$).
Vì $AO$ vuông góc với mặt phẳng $BCDO$ nên theo định lý Pi-ta-go ta có:
$AO = \sqrt {A{B^2} – B{O^2}} $ $ = \sqrt {{a^2} – {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{a}{{\sqrt 2 }}.$
${S_{BCDE}} = {a^2}$ (Vì tứ giác $BCDE$ là hình vuông cạnh $a$).
Do đó ${V_{ABCDEF}} = \frac{2}{3}.{a^2}.\frac{a}{{\sqrt 2 }} = \frac{{\sqrt 2 {a^3}}}{3}.$
Bài 3. Cho hình hộp $ABCD.A’B’C’D’.$ Tính tỉ số thể tích của khối hộp đó và thể tích của khối tứ diện $ACB’D’.$
Lời giải:

Gọi thể tích khối hộp $ABCD.A’B’C’D’$ là $V.$
Ta có:
${V_{B’.ABC}} = \frac{1}{3}{V_{ABC.A’B’C’}} = \frac{1}{6}V.$
${V_{A’.B’D’A}} = \frac{1}{3}{V_{ABD.A’B’D’}} = \frac{1}{6}V.$
${V_{D’.ACD}} = \frac{1}{3}{V_{ACD.A’C’D’}} = \frac{1}{6}V.$
${V_{C’.B’D’C}} = \frac{1}{3}{V_{BCD.B’C’D’}} = \frac{1}{6}V.$
Mặt khác: ${V_{C.AD’B’}}$ $ = V – \left( {{V_{B’ABC}} + {V_{A’B’D’A}} + {V_{DACD’}} + {V_{C’B’D’C}}} \right)$ $ = V – \frac{4}{6}V = \frac{1}{3}V.$
Do đó: $\frac{V}{{{V_{CAD’B’}}}} = 3.$
Bài 4. Cho hình chóp $S.ABC.$ Trên các đoạn thẳng $SA$, $SB$, $SC$ lần lượt lấy ba điểm $A’$, $B’$, $C’$ khác $S.$ Chứng minh rằng: $\frac{{{V_{S.A’B’C’}}}}{{{V_{S.ABC}}}} = \frac{{SA’}}{{SA}}.\frac{{SB’}}{{SB}}.\frac{{SC’}}{{SC}}.$
Lời giải:

Gọi $H$, $H’$ lần lượt là hình chiếu của $A$, $A’$ lên mặt phẳng $(SBC).$ Đặt $\alpha = \widehat {BSC}$, $\beta = (\widehat {SA,mp(SBC)}).$
Ta có: $\frac{{{V_{S.A’B’C’}}}}{{{V_{S.ABC}}}} = \frac{{\frac{1}{3}{S_{\Delta SB’C’}}.A’H’}}{{\frac{1}{3}{S_{\Delta SBC}}.AH}}.$
$ = \frac{{\frac{1}{2}SC’.SB’.\sin \alpha .SA’.\sin \beta }}{{\frac{1}{2}SB.SC.\sin \alpha .SA.\sin \beta }}.$
$ = \frac{{SA’.SB’.SC’}}{{SA.SB.SC}}.$
Hình vẽ này chỉ cho một trường hợp $H$, $H’$ nằm ở miền trong tam giác $SBC.$ Các trường hợp khác được vẽ hình và chứng minh tương tự.
Bài 5. Cho tam giác $ABC$ vuông cân ở $A$ và $AB = a.$ Trên đường thẳng qua $C$ và vuông góc với mặt phẳng $(ABC)$ lấy điểm $D$ sao cho $CD = a.$ Mặt phẳng qua $C$ vuông góc với $BD$ cắt $BD$ tại $F$ và cắt $AD$ tại $E.$ Tính thể tích khối tứ diện $CDEF$ theo $a.$
Lời giải:

Gọi mặt phẳng qua $C$ và vuông góc với $BD$ là $(\alpha ).$
Vì $CF \subset (\alpha )$ nên $BD \bot CF$, tương tự $EF \bot BD.$
Do đó ${V_{D.CEF}} = \frac{1}{3}{S_{\Delta ECF}}.FD$ $(1).$
Mặt khác ta có:
${BA \bot AC}$ (giả thiết).
${BA \bot DC}$ (giả thiết).
Nên $BA \bot (ACD)$ $ \Rightarrow BA \bot CE$ $(a).$
Vì $BD \bot (\alpha )$ nên $BD \bot CE$ $(b).$
Từ $(a)$ và $(b)$ ta có: $CE \bot (ABD).$
$ \Rightarrow CE \bot EF$ $ \Rightarrow $ Tam giác $CEF$ vuông tại đỉnh $E.$
Theo định lý Pi-ta-go ta có: $EF = \sqrt {C{F^2} – C{E^2}} $ $(2).$
Xét tam giác vuông $CBD$ $\left( {\widehat C = {{90}^0}} \right)$, $CF$ là đường cao. Ta có:
$\frac{1}{{C{F^2}}} = \frac{1}{{C{B^2}}} + \frac{1}{{C{D^2}}}$ $ = \frac{1}{{2{a^2}}} + \frac{1}{{{a^2}}} = \frac{3}{{2{a^2}}}.$
$ \Rightarrow C{F^2} = \frac{{2{a^2}}}{3}$ $(3).$
Xét tam giác vuông $CDA$ $\left( {\widehat C = {{90}^0}} \right)$, theo giả thiết tam giác này cân tại $C.$ Vì $CE \bot AD$ nên $E$ là trung điểm của $AD.$ Từ đó suy ra $CE = \frac{1}{2}AD = \frac{{\sqrt 2 a}}{2}.$
$ \Rightarrow C{E^2} = \frac{1}{2}{a^2}$ $(4).$
Thay $(3)$, $(4)$ vào $(2)$ ta có: $EF = \sqrt {\frac{{2{a^2}}}{3} – \frac{1}{2}{a^2}} $ $ = \sqrt {\frac{{{a^2}}}{6}} = \frac{{a\sqrt 6 }}{6}.$
$ \Rightarrow {S_{\Delta EFC}} = \frac{1}{2}EF.EC$ $ = \frac{1}{2}\frac{{a\sqrt 6 }}{6}.\frac{{\sqrt 2 a}}{2} = \frac{{\sqrt 3 {a^2}}}{{12}}$ $(5).$
Mặt khác $F{D^2} = C{D^2} – C{F^2}$ $ = {a^2} – \frac{{2{a^2}}}{3} = \frac{{{a^2}}}{3}$ $ \Rightarrow FD = \frac{a}{{\sqrt 3 }}$ $(6).$
Thay $(5)$, $(6)$ vào $(1)$ ta có: ${V_{D.CEF}} = \frac{1}{3}.\frac{{\sqrt 3 {a^2}}}{{12}}.\frac{a}{{\sqrt 3 }} = \frac{{{a^2}}}{{36}}$ (đvdt).
Bài 6. Cho hai đường thẳng chéo nhau $d$ và $d’.$ Đoạn thẳng $AB$ có độ dài bằng $a$ trượt trên $d$, đoạn thẳng $CD$ có độ dài $b$ trượt trên $d.$ Chứng minh rằng khối tứ diện $ABCD$ có thể tích không đổi.
Lời giải:
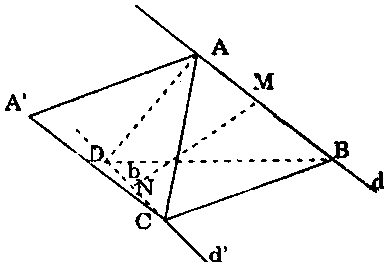
Gọi khoảng cách giữa hai đường thẳng chéo nhau $d$, $d’$ là $h$ và góc của $d$ và $d’$ là $\varphi .$
Trong mặt phẳng $(ABC)$ dựng hình bình hành $CBAA’.$
Ta có $AA’//BC$ nên ${V_{ABCD}} = {V_{A’BCD}}.$
Gọi $MN$ là đoạn vuông góc chung của $AB$ và $CD$ ($M \in AB$, $N \in CD$).
Vì $BM//CA’$ nên ${V_{BA’CD}} = {V_{MA’CD}}.$
Ta có $MN \bot AB$ nên $MN \bot CA’$, hơn nữa $MN \bot CD.$
Do đó $MN \bot \left( {CDA’} \right).$
Chú ý rằng $(\widehat {AB,CD}) = \left( {\widehat {AC’,CD}} \right) = \varphi $ nên:
${V_{MA’CD}} = \frac{1}{3}{S_{\Delta A’CD}}.MN$ $ = \frac{1}{3}.\frac{1}{2}CA’.CD.\sin \varphi .MN$ $ = \frac{1}{6}a.b.h.\sin \varphi .$
$ \Rightarrow {V_{ABCD}} = \frac{1}{6}a.b.h.\sin \varphi .$









