Bài viết hướng dẫn giải các bài tập trong phần câu hỏi và bài tập và phần luyện tập của sách giáo khoa Hình học 12 cơ bản: Khối đa diện lồi và khối đa diện đều.
CÂU HỎI VÀ BÀI TẬP
Bài 2. Cho hình lập phương $(H).$ Gọi $(H’)$ là hình bát diện đều có các đỉnh là tâm các mặt của $(H).$ Tính tỉ số diện tích toàn phần của $(H)$ và $(H’).$
Lời giải:
Giả sử khối lập phương có cạnh bằng $a.$ Khi đó diện tích toàn phần của nó là: ${S_1} = 6{a^2}.$
Xét bát diện đều thu được, khi đó diện tích toàn phần của nó là $8$ lần diện tích tam giác đều $MQE$ (hình vẽ).
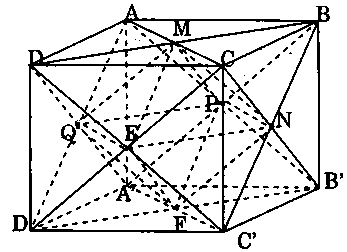
Xét tam giác $ACD’$, ta có $M$, $Q$ lần lượt là trung điểm của $AC$ và $AD’$ nên $MQ$ là đường trung bình của tam giác $ACD’$, do đó $MQ = \frac{1}{2}CD’ = \frac{1}{2}\sqrt 2 a.$
Ta có: ${S_{\Delta MQE}} = \frac{1}{2}{\left( {\frac{1}{2}\sqrt 2 a} \right)^2}.\frac{{\sqrt 3 }}{2}$ $ = \frac{1}{8}{a^2}\sqrt 3 .$
Diện tích xung quanh của bát diện đều là: ${S_2} = 8.\frac{1}{8}.{a^2}\sqrt 3 = {a^2}\sqrt 3 .$
Do đó: $\frac{{{S_1}}}{{{S_2}}} = \frac{{6{a^2}}}{{a\sqrt 3 }} = 2\sqrt 3 .$
Bài 3. Chứng minh rằng tâm của các mặt của hình tứ diện đều là các đỉnh của một hình tứ diện đều.
Lời giải:
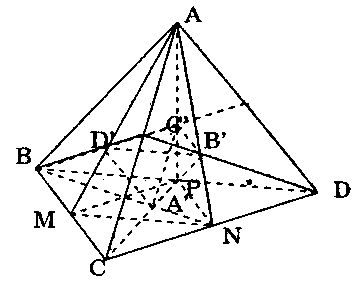
Gọi tâm các mặt đối diện với các đỉnh $A$, $B$, $C$, $D$ lần lượt là $A’$, $B’$, $C’$, $D’.$
Ta sẽ chứng minh cho bốn điểm $A’$, $B’$, $C’$, $D’$ tạo thành tứ diện đều.
Hiển nhiên bốn điểm đó tạo thành một tứ diện.
Gọi trung điểm các cạnh $BC$, $CD$, $DB$ lần lượt là $M$, $N$, $P.$ Dễ thấy: tam giác $AMN$ đồng dạng với tam giác $AD’B’.$
Do đó: $\frac{{D’B’}}{{MN}} = \frac{{AD’}}{{AM}} = \frac{2}{3}.$
$ \Rightarrow D’B’ = \frac{2}{3}MN$ $ = \frac{2}{3}.\frac{{BD}}{2} = \frac{a}{3}$ ($a$ là độ dài cạnh của tứ diện $ABCD$).
Tương tự ta cũng có: $D’C’ = C’B’ = \frac{a}{3}.$
Từ đó tam giác $B’C’D’$ là tam giác đều cạnh bằng $\frac{a}{3}.$
Bằng cách làm hoàn toàn tương tự ta cũng chứng minh được các tam giác $A’B’D’$, $A’B’C’$, $A’C’D’$ cũng là tam giác đều cạnh $\frac{a}{3}.$ Vậy tứ diện $A’B’C’D’$ là tứ diện đều.
Bài 4. Cho hình bát diện đều $ABCDEF.$ Chứng minh rằng:
a) Các đoạn thẳng $AF$, $BD$ và $CE$ đôi một vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
b) $ABFD$, $AEFC$ và $BCDE$ là những hình vuông.
Lời giải:
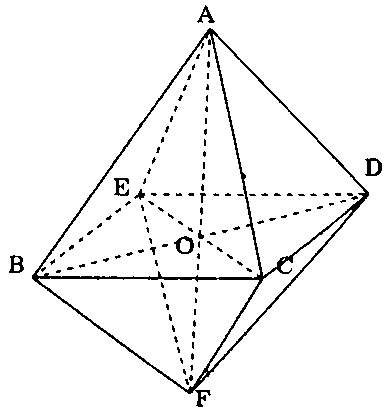
a) Theo giả thiết ta có:
$BE = ED = DC = BC.$
$AE = EF = FC = CA.$
$BF = FD = DA = AB.$
Nên các tứ giác $BEDC$, $BADF$, $AEFC$ là các hình thoi (hiển nhiên chúng là các tứ giác).
Vì vậy $AF$, $FC$, $BD$ đôi một vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
b) Ở câu a ta đã chứng minh được các tứ giác $BEDC$, $ABFD$, $AEFC$ là những hình thoi. Gọi $O$ là giao điểm các đường thẳng $BD$, $EC$, $AF.$
Xét các tam giác $AEC$ và $BEC$, chúng bằng nhau theo trường hợp cạnh – cạnh – cạnh nên $OA = OB$ $ \Leftrightarrow AF = BD$ $ \Rightarrow AEFC$ là hình vuông.
Hoàn toàn tương tự ta có các tứ giác còn lại là hình vuông.









