Bài viết hướng dẫn giải các bài tập trong phần câu hỏi và bài tập và phần luyện tập của sách giáo khoa Hình học 12 nâng cao: Mặt cầu, khối cầu.
CÂU HỎI VÀ BÀI TẬP
Bài 1. Trong không gian cho ba đoạn thẳng $AB$, $BC$, $CD$ sao cho $AB \bot BC$, $BC \bot CD$, $CD \bot AB.$ Chứng minh rằng có mặt cầu đi qua bốn điểm $A$, $B$, $C$, $D.$ Tính bán kính mặt cầu đó nếu $AB = a$, $BC = b$, $CD = c.$
Lời giải:
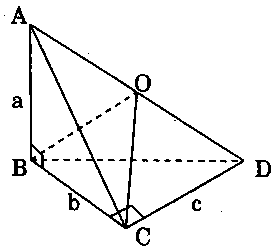
Vì $AB \bot BC$ và $AB \bot CD$ nên $AB \bot BD.$
Tương tự ta có $DC \bot AC.$
Theo tính chất đường trung tuyến của tam giác vuông ứng với cạnh huyền: $BO = CO = \frac{1}{2}AD.$
Suy ra $A$, $B$, $C$, $D$ nằm trên mặt cầu tâm $O$, bán kính: $R = \frac{1}{2}AD$ $ = \frac{1}{2}\sqrt {{a^2} + {b^2} + {c^2}} .$ Tâm mặt cầu $O$ là trung điểm $AD.$
Bài 2.
a) Tìm tập hợp tâm các mặt cầu đi qua hai điểm phân biệt $A$, $B$ cho trước.
b) Tìm tập hợp tâm các mặt cầu đi qua ba điểm $A$, $B$, $C$ đôi một phân biệt cho trước.
c) Tìm tập hợp tâm các mặt cầu đi qua một đường tròn cho trước.
d) Có hay không một mặt cầu đi qua một đường tròn và một điểm nằm ngoài mặt phẳng của đường tròn.
Lời giải:
a) Gọi $I$ là tâm mặt cầu đi qua hai điểm $A$, $B$ cho trước, khi đó $IA = IB.$
Vậy $I$ nằm trên mặt phẳng trung trực của $AB.$
b) $I$ là tâm mặt cầu đi qua ba điểm phân biệt $A$, $B$, $C$ cho trước khi và chỉ khi $IA = IB = IC.$ Vậy:
+ Nếu ba điểm $A$, $B$, $C$ không thẳng hàng thì tập hợp các điểm $I$ là trục của đường tròn ngoại tiếp tam giác $ABC.$
+ Nếu ba điểm $A$, $B$, $C$ thẳng hàng và đôi một phân biệt thì tập hợp $I$ là rỗng.
c) $I$ là tâm mặt cầu đi qua đường tròn $(C)$ cho trước khi và chỉ khi $I$ cách đều mọi điểm của đường tròn. Vậy tập hợp các điểm $I$ là trục của đường tròn $(C).$
d) Gọi $M$ là điểm nằm ngoài mặt phẳng của đường tròn $(C).$ Lấy điểm $A$ nằm trên $(C)$ và gọi $I$ là giao điểm của trục đường tròn và mặt phẳng trung trực của $MA.$ Khi đó mặt cầu tâm $I$, bán kính $R = IA = IM$ là mặt cầu đi qua đường tròn $(C)$ và đi qua điểm $M.$
Bài 3. Cho điểm $M$ nằm trong mặt cầu $(S).$ Trong các mệnh đề sau mệnh đề nào đúng?
a) Mọi mặt phẳng đi qua $M$ đều cắt $(S)$ theo một đường tròn.
b) Mọi đường thẳng qua $M$ đều cắt $(S)$ tại hai điểm phân biệt.
Lời giải:
Cả a và b đều đúng.
Bài 4. Cho đường thẳng $d$ và điểm $A$ không nằm trên $d.$ Xét các mặt cầu đi qua $A$ và có tâm nằm trên $d.$ Chứng minh rằng các mặt cầu đó luôn luôn đi qua một đường tròn cố định.
Lời giải:
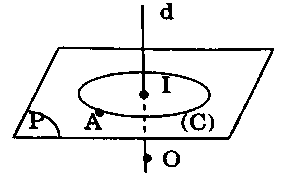
Gọi $S$ là mặt cầu đi qua điểm $A$ có tâm $O$ nằm trên $d$ (Hình vẽ bên). Gọi $(P)$ là mặt phẳng đi qua $A$ và vuông góc với $d.$ Khi đó $(P)$ cắt mặt cầu $S$ theo giao tuyến là đường tròn $(C)$, có tâm $I$ là giao của mặt phẳng $(P)$ với $d$, bán kính $r = IA$, suy ra $(C)$ cố định.
Vậy $S$ luôn đi qua đường tròn cố định $(C).$
Bài 5. Trong các mệnh đề sau đây, mệnh đề nào đúng?
a) Nếu hình đa diện nội tiếp mặt cầu thì mọi mặt của nó là đa giác nội tiếp đường tròn.
b) Nếu các mặt của đa diện nội tiếp đường tròn thì đa diện đó nội tiếp mặt cầu.
Lời giải:
a) Đúng.
b) Sai.

Ví dụ: Cho tứ diện $ABCD$ nội tiếp mặt cầu $S$ (Hình vẽ bên). Lấy điểm $E$ nằm khác phía với $A$ đối với mặt phẳng $(BCD)$ sao cho $E$ không nằm trên $(S).$
Xét hình đa diện $ABCDE$ có $6$ mặt $ABC$, $ABD$, $ADC$, $EBC$, $ECD$, $EDB.$ Các mặt đó đều nội tiếp đường tròn nhưng hình đa diện $ABCDE$ không nội tiếp hình cầu. Vì nếu có mặt cầu đi qua các đỉnh $A$, $B$, $C$, $D$, $E$ thì nó phải đi qua $A$, $B$, $C$, $D$ nên mặt cầu đó chính là $S$, nhưng $E$ lại không nằm trên $S.$
Bài 6.
a) Tìm tập hợp tâm các mặt cầu tiếp xúc với ba cạnh của một tam giác.
b) Chứng minh rằng nếu có mặt cầu tiếp xúc với sáu cạnh của hình tứ diện $ABCD$ thì: $AB + CD$ $= AC + BD$ $= AD + BC.$
Lời giải:
a)
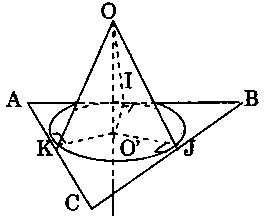
Giả sử $O$ là tâm mặt cầu tiếp xúc với ba cạnh $AB$, $BC$, $CA$ lần lượt tại $I$, $J$, $K$ (Hình bên). Khi đó $OI \bot AB$, $OJ \bot BC$, $OK \bot CA$, $OI = OJ = OK$ $(1).$
Gọi $O’$ là hình chiếu của $O$ lên mp $(ABC)$ thì $(1)$ $ \Leftrightarrow O’I \bot AB$, $O’J \bot BC$, $O’K \bot AC$, $O’I = O’J = O’K$ hay $O’$ là tâm đường tròn nội tiếp tam giác $ABC.$ Suy ra tập hợp các điểm $O$ là trục của đường tròn nội tiếp tam giác $ABC.$
b)
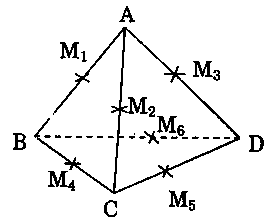
Giả sử có mặt cầu tiếp xúc với $6$ cạnh của tứ diện $ABCD$ tại các điểm ${M_1}$, ${M_2}$, ${M_3}$, ${M_4}$, ${M_5}$, ${M_6}$ như hình vẽ. Khi đó ta có:
$A{M_1} = A{M_2} = A{M_3}$, $B{M_1} = B{M_6} = B{M_4}$, $C{M_5} = C{M_2} = C{M_4}$, $D{M_5} = D{M_3} = D{M_4}.$
Suy ra $A{M_1} + B{M_1} + C{M_5} + D{M_5}$ $ = A{M_2} + C{M_2} + B{M_6} + D{M_6}$ $ = A{M_3} + D{M_3} + B{M_4} + C{M_4}$ $ \Leftrightarrow AB + CD$ $ = AC + BD$ $ = AD + BC.$
Đảo lại nếu tứ diện có tổng các cạnh đối bằng nhau thì tồn tại mặt cầu tiếp xúc với các cạnh của tứ diện.
Bài 7.
a) Tính thể tích khối cầu ngoại tiếp hình chóp tam giác đều cạnh đáy bằng $a$ và chiều cao $h.$
b) Cho hình chóp tứ giác đều $S.ABCD$ có tất cả các cạnh cùng bằng $a.$ Gọi $A’$, $B’$, $C’$, $D’$ lần lượt là trung điểm của các cạnh $SA$, $SB$, $SC$, $SD.$ Chứng minh rằng các điểm $A$, $B$, $C$, $D$, $A’$, $B’$, $C’$, $D’$ cùng thuộc mặt cầu và tính thể tích khối cầu đó.
Lời giải:
a) Giả sử $SH$ là đường cao của hình chóp đều $S.ABC.$ Khi đó $SA = SB = SC$ nên mọi điểm nằm trên $SH$ cách đều $A$, $B$, $C.$
Trong mặt phẳng $(SAH)$ đường trung trực của $SA$ cắt $SH$ tại $O$, thì $O$ là tâm mặt cầu ngoại tiếp hình chóp, bán kính mặt cầu là $R = SO.$
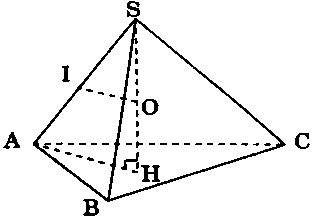
Gọi $I$ là trung điểm $SA$ thì tứ giác $AHOI$ nội tiếp nên:
$SO.SH = SI.SA$ hay $\;SO = \frac{{S{A^2}}}{{2SH}} = \frac{{S{A^2}}}{{2h}}.$
Ta có: $S{A^2} = S{H^2} + A{H^2}$ $ = {h^2} + {\left( {\frac{{a\sqrt 3 }}{3}} \right)^2}$ $ = \frac{{{a^2} + 3{h^2}}}{3}.$
Suy ra $R = SO = \frac{{{a^2} + 3{h^2}}}{{6h}}.$
Vậy thể tích khối cầu $V = \frac{4}{3}\pi {\left( {\frac{{{a^2} + 3{h^2}}}{{6h}}} \right)^2}.$
b)
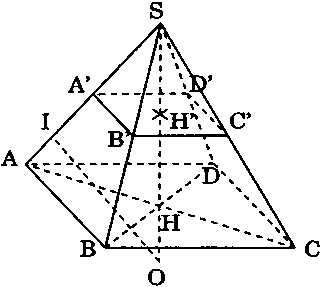
Gọi $SH$ là đường cao của hình chóp đều $SABCD$ thì $H$ là tâm hình vuông $ABCD$ và $SH$ đi qua tâm $H’$ của hình vuông $A’B’C’D’$ (Hình vẽ). Mọi điểm nằm trên $SH$ đều cách đều bốn điểm $A$, $B$, $C$, $D$ và cũng cách đều bốn điểm $A’$, $B’$, $C’$, $D’.$ Trên $SH$ xác định điểm $O$ sao cho $OA = OA’$ thì $O$ cách đều $8$ đỉnh $A$, $B$, $C$, $D$, $A’$, $B’$, $C’$, $D’$ tức $8$ đỉnh đó nằm trên mặt cầu tâm $O$, bán kính $R = OA.$ Điểm $O$ là giao điểm của đường thẳng $SH$ và mặt phẳng trung trực của đoạn $AA’.$
Do $\Delta SAC$ vuông cân tại $S.$ Gọi $I$ là trung điểm $AA’$ thì $\Delta SIO$ cũng vuông cân tại $I$ nên $OI = SI = \frac{{3a}}{4}.$
Suy ra: $R = OA = \sqrt {O{I^2} + A{I^2}} $ $ = \sqrt {{{\left( {\frac{{3a}}{4}} \right)}^2} + {{\left( {\frac{a}{4}} \right)}^2}} $ $ = \frac{{a\sqrt {10} }}{4}.$
Thể tích khối cầu là: $V = \frac{4}{3}\pi {R^3} = \frac{{5\pi {a^3}\sqrt {10} }}{{24}}.$
Bài 8. Cho tứ diện $ABCD$, với $AB = CD = c$, $AC = BD = b$, $AD = BC = a.$
a) Tính diện tích mặt cầu ngoại tiếp tứ diện.
b) Chứng minh rằng có một mặt cầu tiếp xúc với bốn mặt của tứ diện (nó được gọi là mặt cầu nội tiếp tứ diện).
Lời giải:
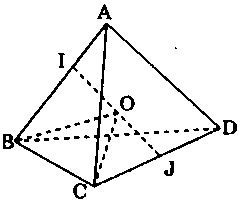
a) Gọi $I$, $J$ lần lượt là trung điểm của $AB$ và $CD$ thì $IJ \bot AB$, $IJ \bot CD.$
Gọi $O$ là trung điểm $IJ$ thì $OA = OB$ và $OC = OD.$
Do $AB = CD = c$ nên hai tam giác vuông $OIB$ và $OJC$ bằng nhau nên $OB = OC.$
Vậy $O$ cách đều $4$ đỉnh $A$, $B$, $C$, $D.$
Mặt cầu ngoại tiếp tứ diện $ABCD$ có tâm $O$, bán kính $R = OA.$
Ta có $O{A^2} = O{I^2} + A{I^2}$ $ = \frac{{I{J^2}}}{4} + \frac{{A{B^2}}}{4}$ $ = \frac{{I{J^2} + {c^2}}}{4}.$
Vì $CI$ là trung tuyến của tam giác $ABC$ nên: $C{I^2} = \frac{{2{a^2} + 2{b^2} – {c^2}}}{4}.$
Suy ra $I{J^2} = C{I^2} – C{J^2}$ $ = \frac{{{a^2} + {b^2} – {c^2}}}{2}.$
Như vậy ${R^2} = O{A^2}$ $ = \frac{{{a^2} + {b^2} + {c^2}}}{8}$ và diện tích mặt cầu ngoại tiếp tứ diện $ABCD$ là: $S = 4\pi {R^2}$ $ = \frac{\pi }{2}\left( {{a^2} + {b^2} + {c^2}} \right).$
b) Các mặt của tứ diện là các tam giác bằng nhau (đều có ba cạnh là $a$, $b$, $c$) nên các đường tròn ngoại tiếp các tam giác đó có bán kính $r$ bằng nhau. Các đường tròn đó đều nằm trên mặt cầu $(O; R)$ nên khoảng cách từ tâm $O$ tới các mặt phẳng chứa các đường tròn đó bằng nhau và bằng: $h = \sqrt {{R^2} – {r^2}} .$ Vậy mặt cầu tâm $O$ bán kính $h$ là mặt cầu nội tiếp tứ diện $ABCD.$
Bài 9. Tìm diện tích mặt cầu ngoại tiếp hình chóp $SABC$ biết $SA = a$, $SB = b$, $SC = c$ và ba cạnh $SA$, $SB$, $SC$ đôi một vuông góc. Chứng minh rằng các điểm $S$, $G$, $I$ thẳng hàng, trong đó $G$ là trọng tâm tam giác $ABC$ và $I$ là tâm mặt cầu ngoại tiếp hình chóp $S.ABC.$
Lời giải:
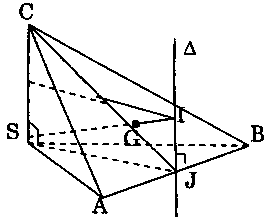
Gọi $J$ là trung điểm của $AB.$ Vì tam giác $SAB$ vuông ở đỉnh $S$ nên $IS = JA = IB$ (Hình vẽ bên).
Gọi $\Delta $ là đường thẳng vuông góc với mặt phẳng $(SAB)$ tại $J$ thì mọi điểm của đường $\Delta $ đều cách đều ba điểm $S$, $A$, $B.$ Bởi vậy nếu gọi $I$ là giao điểm của $\Delta $ với mặt phẳng trung trực của đoạn $SC$ thì $I$ cách đều bốn điểm $S$, $A$, $B$, $C.$
Vậy mặt cầu ngoại tiếp hình chóp $SABC$ có tâm $I$, bán kính $R = IA.$
Ta có: ${R^2} = I{A^2} = I{J^2} + A{J^2}$ $ = {\left( {\frac{{SC}}{2}} \right)^2} + {\left( {\frac{{AB}}{2}} \right)^2}$ $ = \frac{{{a^2} + {b^2} + {c^2}}}{4}.$
Diện tích mặt cầu bằng: $S = 4\pi {R^2}$ $ = \pi \left( {{a^2} + {b^2} + {c^2}} \right).$
Vì $SC // IJ$ nên $SI$ cắt $CJ$ tại điểm $G$ và do $SC = 2IJ$ nên $CG = 2GJ.$ Do $CJ$ là trung tuyến của tam giác $ABC$ nên $G$ là trọng tâm tam giác $ABC.$
Bài 10.
a) Chứng minh rằng một hình lăng trụ có mặt cầu ngoại tiếp khi và chỉ khi nó là hình lăng trụ đứng và đáy là đa giác nội tiếp đường tròn.
b) Trong các hình hộp nội tiếp mặt cầu cho trước, hình hộp nào có diện tích toàn phần lớn nhất.
Lời giải:
a) Nếu $H$ là hình lăng trụ có mặt cầu ngoại tiếp thì các mặt bên là những hình bình hành có đường tròn ngoại tiếp nên phải là hình chữ nhật. Vậy $H$ là hình lăng trụ đứng. Ngoài ra $H$ có mặt cầu ngoại tiếp nên mặt đáy phải là đa giác có đường tròn ngoại tiếp.
Ngược lại cho $H$ là lăng trụ đứng có các đường tròn $(C)$ và $(C’)$ ngoại tiếp các đa giác đáy (Hình vẽ).
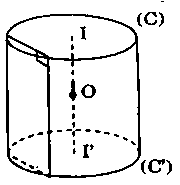
Gọi $I$, $I’$ là tâm của $(C)$ và $(C’)$ thì $II’$ là trục của cả hai đường tròn. Gọi $O$ là trung điểm $II’$ thì $O$ cách đều tất cả các đỉnh của hình lăng trụ đã cho. Vậy hình lăng trụ ấy có mặt cầu ngoại tiếp.
b) Nếu hình hộp $H$ nội tiếp mặt cầu $S(O;R)$ thì các mặt của $H$ phải là những hình chữ nhật, vậy $H$ là hình hộp chữ nhật mà $O$ là giao điểm các đường chéo, và độ dài đường chéo $d = 2R.$
Gọi $a$, $b$, $c$ là các kích thước của hình hộp chữ nhật đó thì ${a^2} + {b^2} + {c^2}$ $ = {d^2} = 4{R^2}.$ Gọi $S$ là diện tích toàn phần của hình hộp thì ta có: $S = 2ab + 2bc + 2ac$ $ \le 2\left( {{a^2} + {b^2} + {c^2}} \right)$ $ = 8{R^2}.$ Vậy $S$ đạt giá trị lớn nhất bằng $8{R^2}$ khi $a = b = c = \frac{{2R}}{{\sqrt 3 }}$, tức là $H$ là hình lập phương.









