Tài liệu gồm 16 trang, được biên soạn bởi quý thầy, cô giáo Nhóm Toán VDC & HSG THPT, hướng dẫn phương pháp giải bài toán Tìm tập xác định của hàm số lũy thừa – mũ – lôgarit có chứa tham số; đây là dạng toán thường gặp trong chương trình Toán 12 phần Giải tích chương 2.
HÀM SỐ LŨY THỪA
1. Định nghĩa: Hàm số y x với được gọi là hàm số lũy thừa.
2. Tập xác định Tập xác định của hàm số y x là với là số nguyên dương với là số nguyên âm hoặc bằng 0 với không nguyên.
3. Đạo hàm Hàm số y x với có đạo hàm với mọi x 0 và 1 x x.
4. Tính chất của hàm số lũy thừa trên khoảng y x 0. Đồ thị hàm số luôn đi qua điểm. Khi x 0 hàm số luôn đồng biến. Trong trường hợp này 0 lim x x do đó đồ thị hàm số không có đường tiệm cận. Khi 1 0 0 y x x hàm số luôn nghịch biến. Trong trường hợp này 0 lim 0 do đó đồ thị hàm số nhận trục Ox là đường tiệm cận ngang và trục Oy là đường tiệm cận đứng.
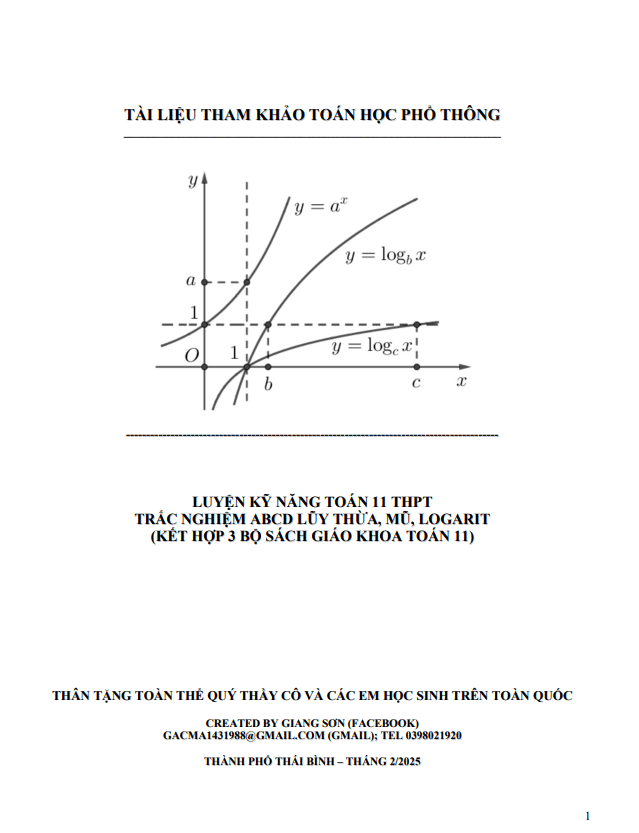
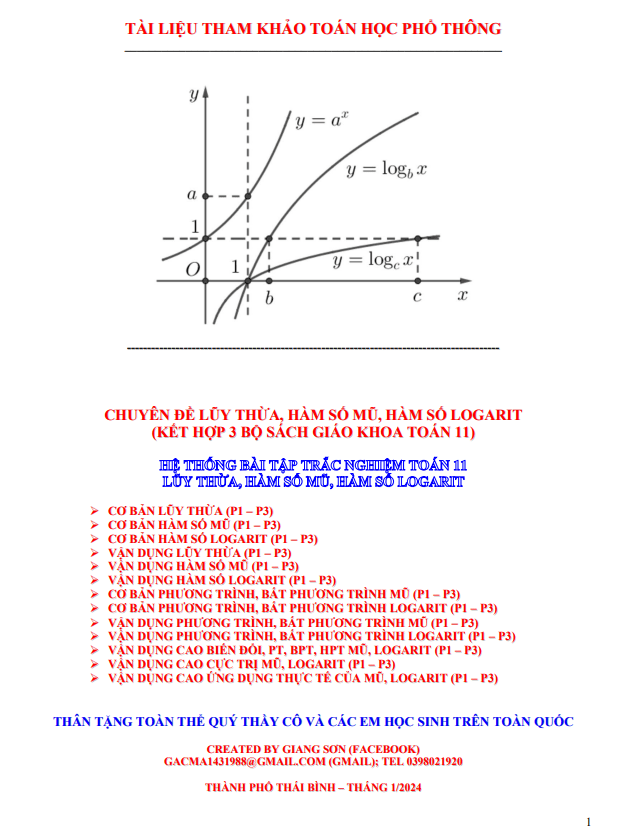
5. Đồ thị hàm số lũy thừa a y x trên khoảng 0 Đồ thị hàm số y x luôn đi qua điểm I.
HÀM SỐ MŨ
1. Định nghĩa: Cho số thực dương a 1. Hàm số x y a được gọi là hàm số mũ cơ số a.
2. Tập xác định: P x y a xác định khi P x xác định. Đối với y a thì có D. Tập giá trị của hàm số mũ là T.
3. Đạo hàm: Công thức thừa nhận.
4. Đồ thị hàm số mũ: x y a. Đồ thị hàm số nhận trục hoành làm tiệm ngang. Đồ thị hàm số đi qua điểm (0;1) và (1;a) nằm về phía bên trên trục hoành x y a x.
HÀM SỐ LÔGARIT
1. Định nghĩa Hàm số dạng log a y x a a được gọi là hàm số logarit cơ số a.
2. Tập xác định và tập giá trị Tập xác định: D 0. Tập giá trị: T.
3. Tính đơn điệu và đồ thị Khi a 1 thì hàm số loga y x đồng biến trên D khi đó nếu log log a a f x g x f x g x Khi 0 1 a thì hàm số loga y x nghịch biến trên D khi đó nếu: log log.
File WORD (dành cho quý thầy, cô): TẢI XUỐNG